
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析: (1)利用导数的几何意义,分别求出切线PA,PB的斜率,再写出直线方程,求出交点P的坐标,联立直线AB的方程和抛物线方程,求出![]() ,即P点纵坐标为定值
,即P点纵坐标为定值![]() ,得证; (2)假设直线AB的方程
,得证; (2)假设直线AB的方程![]() ,联立直线和抛物线方程,求出
,联立直线和抛物线方程,求出![]() ,由两点间的距离公式,得到
,由两点间的距离公式,得到![]() ,化简
,化简![]() ,得出值.
,得出值.
试题解析:(Ⅰ)抛物线![]() ,则
,则![]() ,
,
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() ,同理切线
,同理切线![]() 的方程为
的方程为![]() ,
,
联立得点![]()
![]() , 设直线
, 设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() 。所以
。所以![]() 所以点
所以点![]() 在直线
在直线![]() 上
上
(Ⅱ) 设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() 。
。
![]() ,所以
,所以![]() ,
,
![]()
![]()
![]()
点睛:本题主要考查直线与抛物线位置关系, 属于中档题. 本题思路): (1)由导数求出切线PA,PB方程, 得出交点P坐标, 联立直线AB的方程和抛物线方程, 由韦达定理得出![]() 为定值,即点P纵坐标为定值; (2) 假设直线AB的方程
为定值,即点P纵坐标为定值; (2) 假设直线AB的方程![]() ,联立直线和抛物线方程,由
,联立直线和抛物线方程,由![]() ,求出
,求出![]() 之间的关系,化简
之间的关系,化简![]() ,将
,将![]() 之间的关系代入,求出值.
之间的关系代入,求出值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:

(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序的功能是( )
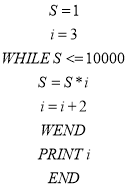
A. 求1×2×3×4×…×10 00的值
B. 求2×4×6×8×…×10 000的值
C. 求3×5×7×9×…×10 001的值
D. 求满足1×3×5×…×n>10 000的最小正整数n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中第五项的系数与第三项的系数的比是10∶1.
的展开式中第五项的系数与第三项的系数的比是10∶1.
(1)求展开式中各项系数的和;
(2)求展开式中含![]() 的项;
的项;
(3)求展开式中系数最大的项和二项式系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次招聘中,主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题。甲能正确完成其中的4道题,乙能正确完成每道题的概率为![]() ,且每道题完成与否互不影响。
,且每道题完成与否互不影响。
⑴记所抽取的3道题中,甲答对的题数为X,则X的分布列为____________;
⑵记乙能答对的题数为Y,则Y的期望为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
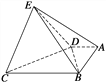
(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人同时从![]() 地赶住
地赶住![]() 地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达
地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达![]() 地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开
地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开![]() 地的距离
地的距离![]() 与所用时间
与所用时间![]() 的函数关系用图象表示如下:
的函数关系用图象表示如下:

则上述四个函数图象中,甲、乙两人运行的函数关系的图象应该分别是( )
A. 图①、图② B. 图①、图④ C. 图③、图② D. 图③、图④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com