
【题目】已知实数![]() 满足
满足 ,若
,若![]() 只在点(4,3)处取得最大值,则
只在点(4,3)处取得最大值,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
由约束条件作出可行域,然后对a进行分类,当a≥0时显然满足题意,当a<0时,化目标函数为直线方程斜截式,比较其斜率与直线BC的斜率的大小得到a的范围.
由不等式组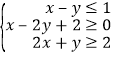 作可行域如图:
作可行域如图:
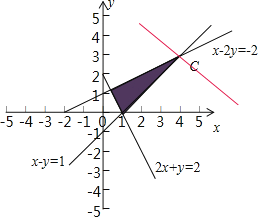
联立![]() ,解得C(4,3).
,解得C(4,3).
当a=0时,目标函数化为z=x,由图可知,
可行解(4,3)使z=x﹣ay取得最大值,符合题意;
当a>0时,由z=x﹣ay,得y=![]() x
x![]() ,此直线斜率大于0,当在y轴上截距最大时z最大,
,此直线斜率大于0,当在y轴上截距最大时z最大,
可行解(4,3)为使目标函数z=x﹣ay的最优解,
a<1符合题意;
当a<0时,由z=x﹣ay,得y=![]() x
x![]() ,此直线斜率为负值,
,此直线斜率为负值,
要使可行解(4,3)为使目标函数z=x﹣ay取得最大值的唯一的最优解,则![]() <0,即a<0.
<0,即a<0.
综上,实数a的取值范围是(﹣∞,1).
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某家具厂生产一种办公桌,每张办公桌的成本为100元,出厂单价为160元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部办公桌出厂单价降低1元.根据市场调查,销售商一次订购量不会超过160张.
(1)设一次订购量为![]() 张,办公桌的实际出厂单价为
张,办公桌的实际出厂单价为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)当一次性订购量![]() 为多少时,该家具厂这次销售办公桌所获得的利润
为多少时,该家具厂这次销售办公桌所获得的利润![]() 最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司有750辆电动汽车供租赁使用,管理这些电动汽车的费用是每日![]() 元.根据调查发现,若每辆电动汽车的日租金不超过90元,则电动汽车可以全部租出;若超过90元,则每超过1元,租不出去的电动汽车就增加3辆.设每辆电动汽车的日租金为
元.根据调查发现,若每辆电动汽车的日租金不超过90元,则电动汽车可以全部租出;若超过90元,则每超过1元,租不出去的电动汽车就增加3辆.设每辆电动汽车的日租金为![]() 元(
元(![]() ),用
),用![]() (单位:元)表示出租电动汽车的日净收入.(日净收入等于日出租电动汽车的总收入减去日管理费用)
(单位:元)表示出租电动汽车的日净收入.(日净收入等于日出租电动汽车的总收入减去日管理费用)
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)试问当每辆电动汽车的日租金为多少元时?才能使日净收入最多,并求出日净收入的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的某车间共有![]() 位工人,其中
位工人,其中![]() 的人爱好运动。经体检调查,这
的人爱好运动。经体检调查,这![]() 位工人的健康指数(百分制)如下茎叶图所示。体检评价标准指出:健康指数不低于
位工人的健康指数(百分制)如下茎叶图所示。体检评价标准指出:健康指数不低于![]() 者为“身体状况好”,健康指数低于
者为“身体状况好”,健康指数低于![]() 者为“身体状况一般”。
者为“身体状况一般”。

(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“身体状况好与爱好运动有关系”?
列联表,并判断有多大把握认为“身体状况好与爱好运动有关系”?
身体状况好 | 身体状况一般 | 总计 | |
爱好运动 | |||
不爱好运动 | |||
总计 |
|
(2)现将![]() 位工人的健康指数分为如下
位工人的健康指数分为如下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示。计算该车间中工人的健康指数的平均数,由茎叶图得到真实值记为
,其频率分布直方图如图所示。计算该车间中工人的健康指数的平均数,由茎叶图得到真实值记为![]() ,由频率分布直方图得到估计值记为
,由频率分布直方图得到估计值记为![]() ,求
,求![]() 与
与![]() 的误差值;
的误差值;
(3)以该车间的样本数据来估计该厂的总体数据,若从该厂健康指数不低于![]() 者中任选
者中任选![]() 人,设
人,设![]() 表示爱好运动的人数,求
表示爱好运动的人数,求![]() 的数学期望。
的数学期望。
附:![]() 。
。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,
时,![]() .
.

(1)作出![]() 的图象;
的图象;
(2)求![]() 的解析式;
的解析式;
(3)若关于x的方程![]() 有解,将方程所有解的和记作M,结合(1)中的图象,求M的值.
有解,将方程所有解的和记作M,结合(1)中的图象,求M的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() ,
,![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)定义:曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .若抛物线
.若抛物线![]() 上存在点
上存在点![]() (不与原点重合)处的切线交椭圆于
(不与原点重合)处的切线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .直线
.直线![]() 与过点
与过点![]() 且平行于
且平行于![]() 轴的直线的交点为
轴的直线的交点为![]() ,证明:点
,证明:点![]() 必在定直线上.
必在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com