
【题目】函数f(x)=2sin(ωx+φ)(ω>0,|φ|<![]() )的一个零点为
)的一个零点为![]() ,其图象距离该零点最近的一条对称轴为x=
,其图象距离该零点最近的一条对称轴为x=![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若关于x的方程f(x)+log2k=0在x∈[![]() ,
,![]() ]上恒有实数解,求实数k的取值范围.
]上恒有实数解,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】某产品自生产并投入市场以来,生产企业为确保产品质量,决定邀请第三方检测机构对产品进行质量检测,并依据质量指标![]() 来衡量产品的质量.当
来衡量产品的质量.当![]() 时,产品为优等品;当
时,产品为优等品;当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标
时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标![]() 的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
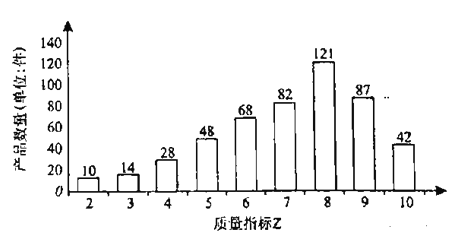
(1)从该企业生产的所有产品中随机抽取1件,求该产品为优等品的概率;
(2)现某人决定购买80件该产品.已知每件成本1000元,购买前,邀请第三方检测机构对要购买的80件产品进行抽样检测.买家、企业及第三方检测机构就检测方案达成以下协议:从80件产品中随机抽出4件产品进行检测,若检测出3件或4件为优等品,则按每件1600元购买,否则按每件1500元购买,每件产品的检测费用250元由企业承担.记企业的收益为![]() 元,求
元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)商场为推广此款产品,现面向意向客户推出“玩游戏,送大奖”活动.客户可根据抛硬币的结果,操控机器人在方格上行进,已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从
,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从![]() 到
到![]() ),若掷出反面,机器人向前移动两格(从
),若掷出反面,机器人向前移动两格(从![]() 到
到![]() ),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第
),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否吸引顾客购买该款产品.
是等比数列,并解释此方案能否吸引顾客购买该款产品.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}中,前n项和![]() .
.
(1)求数列{an}的通项公式;
(2)若![]() 恒成立,求k的取值范围;
恒成立,求k的取值范围;
(3)是否存在正整数m,k,使得am,am+5,ak成等比数列?若存在,求出m和k的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响,已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分,经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.
表1
文章学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com