Question

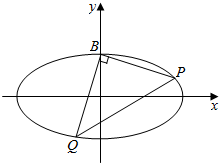
12．如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率是$\frac{{\sqrt{3}}}{2}$，一个顶点是B（0，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设P，Q是椭圆C上异于点B的任意两点，且BP⊥BQ．试问：直线PQ是否恒过一定点？若是，求出该定点的坐标；若不是，说明理由．

Answer 1

分析 （Ⅰ）设椭圆C的半焦距为c．求出b利用离心率求出a，即可求解椭圆C的方程．
（Ⅱ）证法一：直线PQ的斜率存在，设其方程为y=kx+m．将直线PQ的方程代入x²+4y²=4，
消去y，设 P（x₁，y₁），Q（x₂，y₂），利用韦达定理，通过BP⊥BQ，化简求出5m²-2m-3=0，求出m，即可得到直线PQ恒过的定点．
证法二：直线BP，BQ的斜率均存在，设直线BP的方程为y=kx+1，将直线BP的方程代入x²+4y²=4，消去y，解得x，设 P（x₁，y₁），转化求出P的坐标，求出Q坐标，求出直线PQ的方程利用直线系方程求出定点坐标．

解答 （本小题满分14分）
（Ⅰ）解：设椭圆C的半焦距为c．依题意，得b=1，（1分）
且 ${e^2}=\frac{c^2}{a^2}=\frac{{{a^2}-1}}{a^2}=\frac{3}{4}$，（3分）
解得 a²=4．（4分）
所以，椭圆C的方程是$\frac{x^2}{4}+{y^2}=1$．（5分）
（Ⅱ）证法一：易知，直线PQ的斜率存在，设其方程为y=kx+m．（6分）
将直线PQ的方程代入x²+4y²=4，
消去y，整理得 （1+4k²）x²+8kmx+4m²-4=0．（8分）
设 P（x₁，y₁），Q（x₂，y₂），
则 ${x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}}$，${x_1}•{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$．①（9分）
因为 BP⊥BQ，且直线BP，BQ的斜率均存在，
所以 $\frac{{{y_1}-1}}{x_1}•\frac{{{y_2}-1}}{x_2}=-1$，整理得 x₁x₂+y₁y₂-（y₁+y₂）+1=0．②（10分）
因为 y₁=kx₁+m，y₂=kx₂+m，
所以 y₁+y₂=k（x₁+x₂）+2m，${y_1}{y_2}={k^2}{x_1}{x_2}+mk（{x_1}+{x_2}）+{m^2}$．③
将③代入②，整理得$（1+{k^2}）{x_1}{x_2}+k（m-1）（{x_1}+{x_2}）+{（m-1）^2}=0$．④（11分）
将①代入④，整理得 5m²-2m-3=0．（13分）
解得 $m=-\frac{3}{5}$，或m=1（舍去）．
所以，直线PQ恒过定点$（0，-\frac{3}{5}）$．（14分）
证法二：直线BP，BQ的斜率均存在，设直线BP的方程为y=kx+1．（6分）
将直线BP的方程代入x²+4y²=4，消去y，得 （1+4k²）x²+8kx=0．（8分）
解得 x=0，或$x=\frac{-8k}{{1+4{k^2}}}$．（9分）
设 P（x₁，y₁），所以${x_1}=\frac{-8k}{{1+4{k^2}}}$，${y_1}=k{x_1}+1=\frac{{1-4{k^2}}}{{1+4{k^2}}}$，
所以 $P（\frac{-8k}{{1+4{k^2}}}，\frac{{1-4{k^2}}}{{1+4{k^2}}}）$．（10分）
以$-\frac{1}{k}$替换点P坐标中的k，可得 $Q（\frac{8k}{{4+{k^2}}}，\frac{{{k^2}-4}}{{{k^2}+4}}）$．（11分）
从而，直线PQ的方程是 $\frac{{y-\frac{{1-4{k^2}}}{{1+4{k^2}}}}}{{\frac{{1-4{k^2}}}{{1+4{k^2}}}-\frac{{{k^2}-4}}{{{k^2}+4}}}}=\frac{{x+\frac{8k}{{1+4{k^2}}}}}{{\frac{-8k}{{1+4{k^2}}}-\frac{8k}{{4+{k^2}}}}}$．
依题意，若直线PQ过定点，则定点必定在y轴上．（13分）
在上述方程中，令x=0，解得$y=-\frac{3}{5}$．
所以，直线PQ恒过定点$（0，-\frac{3}{5}）$．（14分）

点评 本题考查椭圆的标准方程的求法，直线与椭圆的位置关系的综合应用，考查转化思想以及计算能力，难度比较大，是压轴题．