
【题目】已知函数f(x)是定义在(-2,2)上的奇函数.当x∈(-2,0)时,f(x)=-loga(-x)-loga(2+x),其中a>1.
(1)求函数f(x)的零点.
(2)若t∈(0,2),判断函数f(x)在区间(0,t]上是否有最大值和最小值.若有,请求出最大值和最小值,并说明理由.
【答案】(1)函数f(x)的零点为-1,0,1;(2)f(x)有最大值,无最小值,理由见解析.
【解析】
(1)由奇函数![]() 在零点有意义则
在零点有意义则![]() ,然后在
,然后在![]() 上解方程
上解方程![]() ,最后利用奇函数对称性即可求出函数
,最后利用奇函数对称性即可求出函数![]() 的零点.
的零点.
(2)由奇函数的性质求出函数解析式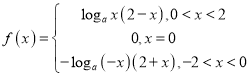 ,然后分别讨论
,然后分别讨论![]() ,和
,和![]() 时,函数
时,函数![]() 在
在![]() 上的最值.
上的最值.
(1)令-loga(-x)-loga(2+x)=0,即![]() ,
,
则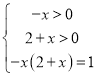 ,解得x=-1.
,解得x=-1.
由题意f(x)是定义在(-2,2)上的奇函数,∴![]() ,
,![]() ,
,
∴f(x)=0解集为{-1,0,1},故函数f(x)的零点为-1,0,1.
(2)∵f(x)是定义在(-2,2)上的奇函数,
∴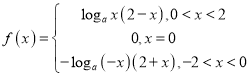
当0<t≤1时,f(x)=logax(2-x)在区间(0,t]上单调递增,
∴f(x)有最大值,f(x)max=f(t)=logat(2-t),无最小值,
当1<t<2时,f(x)=logax(2-x)在区间(0,1]上单调递增,在区间(1,t]上单调递减,∴f(x)有最大值,f(x)max=f(1)=0,无最小值.


科目:高中数学 来源: 题型:
【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-![]() .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,其中喜欢盲拧的30人中男性22人,女性人数正好等于男性不喜欢盲拧人数.
(1)请完成下面的![]() 列联表
列联表
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | |||
女 | |||
总计 |
并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(2)现邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如下表所示.
成功完成时间(分钟) |
|
|
|
|
人数 | 10 | 3 | 5 | 2 |
现从表中成功完成时间在![]() 和
和![]() 这两组内的7名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的7名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及参考数据: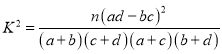 ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
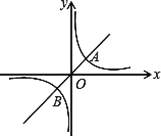
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100![]() ,水温
,水温![]() 与时间
与时间![]() 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度![]() 与时间
与时间![]() 近似满足函数的关系式为
近似满足函数的关系式为 ![]() (
(![]() 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40![]() 时,口感最佳,某天室温为
时,口感最佳,某天室温为![]() 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为

A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),M为
为参数),M为![]() 上的动点,P点满足
上的动点,P点满足![]() ,点P的轨迹为曲线
,点P的轨迹为曲线![]() .
.
(I)求![]() 的方程;
的方程;
(II)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为A,与
的异于极点的交点为A,与![]() 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是2km.如图所示表示甲同学从家出发到乙同学家经过的路程y(km)与时间x(min)的关系,下列结论正确的是( )
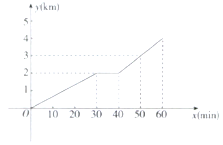
A.甲同学从家出发到乙同学家走了60min
B.甲从家到公园的时间是30min
C.甲从家到公园的速度比从公园到乙同学家的速度快
D.当![]() 时,y与x的关系式为
时,y与x的关系式为![]()
E.当![]() 时,y与x的关系式为
时,y与x的关系式为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com