
【题目】已知函数f(x)=alnx![]() 1,g(x)=x3
1,g(x)=x3![]() 3tx+1(t>0).
3tx+1(t>0).
(1)当a![]() 时,求f(x)在区间[
时,求f(x)在区间[![]() ,e]上的最值;
,e]上的最值;
(2)讨论函数f(x)的单调性;
(3)若g(x)≤xex﹣m+2(e为自然对数的底数)对任意x∈[0,+∞)恒成立时m的最大值为1,求t的取值范围.
【答案】(1)最小值![]() ,最大值为
,最大值为![]() (2)见解析 (3)(0,
(2)见解析 (3)(0,![]() ]
]
【解析】
(1)当a![]() 时,求出
时,求出![]() ,解不等式
,解不等式![]() ,进而求出函数的单调区间,求出函数极值,即可得出结论;
,进而求出函数的单调区间,求出函数极值,即可得出结论;
(2)根据![]() (或
(或![]() )能否恒成立对
)能否恒成立对![]() 分类讨论,若恒成立,得到单调区间,若不恒成立,求出
分类讨论,若恒成立,得到单调区间,若不恒成立,求出![]() ,即可求出单调区间;
,即可求出单调区间;
(3)将所求的不等式分离参数,得到m-1≤(ex﹣x2![]() 对x∈[0,+∞)恒成立,且m的最大值为1,即
对x∈[0,+∞)恒成立,且m的最大值为1,即![]() 恒成立,构造函数
恒成立,构造函数![]() ,求出
,求出![]() 最小值,即可求解.
最小值,即可求解.
(1)当a![]() 时,f(x)
时,f(x)![]() lnx
lnx![]() 1,
1,
∴f′(x)![]() ,(x>0),
,(x>0),
当x![]() 时,f′(x)<0,f(x)单调递减,
时,f′(x)<0,f(x)单调递减,
当x∈(1,e]时,f′(x)>0,f(x)单调递增,
故当x=1时,f(x)取得最小值f(1)![]() ,
,
∵f(e)![]() ,f(
,f(![]() )
)![]() ,
,
∴f(e)>f(![]() ),
),
故函数的最大值为f(e)![]() ,
,
(2)∵f′(x)![]() ,
,
①当a+1≥0即a≥﹣1时,f′(x)>0恒成立,
故f(x)在(0,+∞)上单调递增,
②当a+1<0即a<﹣1时,x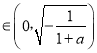 ,f′(x)>0,
,f′(x)>0,
x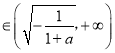 ,f′(x)<0成立,
,f′(x)<0成立,
故f(x)在(0,![]() )上单调递增,
)上单调递增,
故f(x)在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
综上:当a≥﹣1时,![]() 的递增区间是
的递增区间是![]()
当a<﹣1时,f(x)单调递增区间是(0,![]() ),
),
单调递减区间是(![]() ,+∞).
,+∞).
(3)∵g(x)≤xex﹣m+2对任意x∈[0,+∞)恒成立时m的最大值为1,
∴x3![]() 3tx+1≤xex﹣m+2对任意x∈[0,+∞)恒成立,
3tx+1≤xex﹣m+2对任意x∈[0,+∞)恒成立,
∴m-1≤xex﹣x3![]() 3tx=(ex﹣x2
3tx=(ex﹣x2![]()
对任意x∈[0,+∞)恒成立,且m的最大值为1,
令g(x)=ex﹣x2![]() ,
,![]() ,
,
令![]() ,∴
,∴![]() ,
,
当x∈(0,ln2)时,h′(x)=ex﹣2<0,h(x)单调递减,
当x∈(ln2,+∞)时,h′(x)=ex﹣2>0,h(x)单调递增,
![]() ,故
,故![]() ,
,
故g(x)单调递增,g(x)≥g(0)=1﹣3t≥0,∴0<t![]()
即t的取值范围(0,![]() ].
].


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
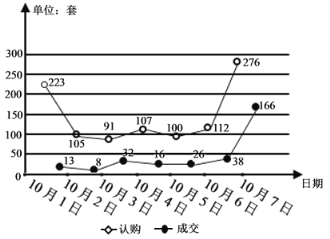
【题目】某地在国庆节![]() 天假期中的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这
天假期中的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这![]() 天的认购量与成交量作出如下判断:①成交量的中位数为
天的认购量与成交量作出如下判断:①成交量的中位数为![]() ;②认购量与日期正相关;③日成交量超过日平均成交量的有
;②认购量与日期正相关;③日成交量超过日平均成交量的有![]() 天,则上述判断中正确的个数为( )
天,则上述判断中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年年底,三部进口影片![]() 登录银屏,包括《海王》,《龙猫》和《蜘蛛侠》,经过了解,
登录银屏,包括《海王》,《龙猫》和《蜘蛛侠》,经过了解,![]() 电影比《蜘蛛侠》早上映一周,
电影比《蜘蛛侠》早上映一周,![]() 电影的票房比《龙猫》高,《蜘蛛侠》的票房比
电影的票房比《龙猫》高,《蜘蛛侠》的票房比![]() 电影低,据此可以判断( )
电影低,据此可以判断( )
A.![]() 是《海王》,
是《海王》,![]() 是《蜘蛛侠》,
是《蜘蛛侠》,![]() 是《龙猫》
是《龙猫》
B.![]() 是《蜘蛛侠》,
是《蜘蛛侠》,![]() 是《龙猫》,
是《龙猫》,![]() 是《海王》
是《海王》
C.![]() 是《龙猫》,
是《龙猫》,![]() 是《海王》,
是《海王》,![]() 是《蜘蛛侠》
是《蜘蛛侠》
D.![]() 是《龙猫》,
是《龙猫》,![]() 是《蜘蛛侠》,
是《蜘蛛侠》,![]() 是《海王》
是《海王》
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回收1吨废纸可以生产出0.8吨再生纸,可能节约用水约100吨,节约用煤约1.2吨,回收1吨废铅蓄电池可再生铅约0.6吨,可节约用煤约0.8吨,节约用水约120吨,回收每吨废铅蓄电池的费用约0.9万元,回收1吨废纸的费用约为0.2万元.现用于回收废纸和废铅蓄电池的费用不超过18万元,在保证节约用煤不少于12吨的前提下,最多可节约用水约__________吨.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
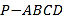
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)直线l与曲线C是否有公共点?并说明理由;
(2)若直线l与两坐标轴的交点为A,B,点P是曲线C上的一点,求△PAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() :
:![]() 与椭圆
与椭圆![]() :
:![]() 满足
满足![]() ,则称这两个椭圆相似,
,则称这两个椭圆相似,![]() 叫相似比.若椭圆
叫相似比.若椭圆![]() 与椭圆
与椭圆![]() 相似且过
相似且过![]() 点.
点.
(I)求椭圆![]() 的标准方程;
的标准方程;
(II)过点![]() 作斜率不为零的直线
作斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 的右焦点,直线
的右焦点,直线![]() 、
、![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据我市房地产数据显示,今年我市前5个月新建住宅销售均价逐月上升,为抑制房价过快上涨,政府从6月份开始推出限价房等宏观调控措施,6月份开始房价得到很好的抑制,房价回落.今年前10个月的房价均价如表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
均价y(万元/平方米) | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
地产数据研究发现,从1月份至5月份的各月均价y(万元/平方米)与x之间具有正线性相关关系,从6月份至10月份的各月均价y(万元/平方米)与x之间具有负线性相关关系.
(1)若政府不调控,根据前5个月的数据,求y关于x的回归直线方程,并预测12月份的房地产均价.(精确到0.01)
(2)政府调控后,从6月份至10月份的数据可得到y与x的回归直线方程为:![]() .由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)
.由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)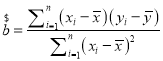 ;
;![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com