
����Ŀ��ij��˾�����µļס��������ŵ���1��9�·ݵ�Ӫҵ���λ����Ԫ������ͳ�Ʋ��õ���ͼ����ͼ.

������������ŵ�Ӫҵ��ķ����У��������( )
A.���ŵ��Ӫҵ������ͼ���нϺõĶԳ��ԣ��ʶ�Ӫҵ���ƽ��ֵԼΪ32��Ԫ
B.���ݼ��ŵ��Ӫҵ������ͼ��֪�����ŵ�Ӫҵ���ƽ��ֵ��[20��25]��
C.�������ŵ��Ӫҵ������ͼ��֪����Ӫҵ����������������
D.���ŵ�����9���·��е�Ӫҵ��ļ���Ϊ25��Ԫ
���𰸡�A
��������
��������ͼ�����ж�ÿ��ѡ����ŵ��Ӫҵ��ƽ��ֵԶ����32��Ԫ��A����������ȷ���õ���.
����A�����ŵ��Ӫҵ������ͼ���нϺõĶԳ��ԣ�Ӫҵ��ƽ��ֵԶ����32��Ԫ��A����.
����B�����ŵ��Ӫҵ���ƽ��ֵΪ![]() 21.6��
21.6��
�����ŵ�Ӫҵ���ƽ��ֵ������[20��25]�ڣ�B��ȷ.
����C���������ŵ��Ӫҵ������ͼ��֪����Ӫҵ���������������ƣ�C��ȷ.
����D�����ŵ�����9�����е�Ӫҵ�����ֵΪ30��Ԫ����СֵΪ5��Ԫ��
��Ϊ25��Ԫ��D��ȷ.
��ѡ��A.


 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���乫˾ÿ��������ij������![]() ���ʣ��ù�˾��8������Ϊ
���ʣ��ù�˾��8������Ϊ![]() ��
��![]() �Ϳ�����4������Ϊ
�Ϳ�����4������Ϊ![]() ��
��![]() �Ϳ�������10����ʻԱ��ÿ������ÿ�������Ĵ���Ϊ
�Ϳ�������10����ʻԱ��ÿ������ÿ�������Ĵ���Ϊ![]() �Ϳ���4�Σ�
�Ϳ���4�Σ�![]() �Ϳ���3�Σ�ÿ������ÿ�������ijɱ�Ϊ
�Ϳ���3�Σ�ÿ������ÿ�������ijɱ�Ϊ![]() �Ϳ���320Ԫ��
�Ϳ���320Ԫ��![]() �Ϳ���504Ԫ������Ϊ�ù�˾�������䳵����ʹ�˷ѳɱ���ͣ�����˷��Ƕ��٣�
�Ϳ���504Ԫ������Ϊ�ù�˾�������䳵����ʹ�˷ѳɱ���ͣ�����˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˸����һ�Σ�����Ŀ��ĸ��ʷֱ���![]() ��
��![]() ��������������Ƿ����Ŀ�꣬�֮��û��Ӱ�죻ÿ������Ƿ����Ŀ�꣬�֮��û��Ӱ�죮
��������������Ƿ����Ŀ�꣬�֮��û��Ӱ�죻ÿ������Ƿ����Ŀ�꣬�֮��û��Ӱ�죮
��1��������4�Σ�����1��δ����Ŀ��ĸ��ʣ�
��2�������˸����4�Σ���ǡ�û���Ŀ��2������ǡ�û���Ŀ��3�εĸ��ʣ�
��3������ij������2��δ����Ŀ�꣬��ֹͣ���������ǡ�����5�κ���ֹ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ƽ���ı���ABCD�У�A(1��1)��![]() ��(6��0)����M���߶�AB���е㣬�߶�CM��BD���ڵ�P��(1) ��
��(6��0)����M���߶�AB���е㣬�߶�CM��BD���ڵ�P��(1) ��![]() ��(3��5)�����C�����ꣻ(2) ��|
��(3��5)�����C�����ꣻ(2) ��|![]() |��|
|��|![]() |ʱ�����P�Ĺ켣��
|ʱ�����P�Ĺ켣��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪0��m��2,����M��������F1����m,0��,F2��m,0���ľ���֮��Ϊ4,���M�Ĺ켣Ϊ����C,������C����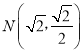 .
.
��1����m��ֵ�Լ�����C�ķ��̣�
��2��������![]() ��б�ʲ�Ϊ���ֱ��l������C����A,B����.֤������ABΪֱ����Բ������C���Ҷ���.
��б�ʲ�Ϊ���ֱ��l������C����A,B����.֤������ABΪֱ����Բ������C���Ҷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4λͬѧ��ͬһ������硢����μӡ����������ء���������Զ�����λ���������������̨�ס�5����Ŀ�IJ��ԣ�ÿλͬѧ���硢���������1����Ŀ���Ҳ��ظ�.�����粻�⡰��������Ŀ�����粻�⡰̨�ס���Ŀ��������Ŀ���硢���綼������1�ˣ���ͬ�İ��ŷ�ʽ�ж����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(3��+7��+8��)��֪��a1Ϊ���������{an}���㣺an��1��.
��1����a1��1��c��1��d��3ʱ��������{an}��ͨ�ʽ��
��2����0��a1��1��c��1��d��3ʱ������a1��ʾ����{an}��ǰ100��ĺ�S100��
��3����0��a1����m������������c����d��3mʱ����֤������a2����a3m+2����a6m+2����a9m+2���ɵȱ����е��ҽ���d��3m.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com