
| A. | x=0 | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{4}$ | D. | x=$\frac{π}{2}$ |
分析 利用两角和差的正弦公式化简函数的解析式,利用函数y=Asin(ωx+φ)的图象变换规律求得所得图象对应的函数解析式,再利用正弦函数的图象的对称性,得出结论.
解答 解:将函数f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$) 的图象向左平移$\frac{π}{6}$个单位,
所得图象对应的函数解析式为y=2sin[2(x+$\frac{π}{6}$)-$\frac{π}{6}$)]=2sin(2x+$\frac{π}{6}$),
令2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,x=$\frac{kπ}{2}$+$\frac{π}{6}$,可得函数的图象的对称轴方程为 x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
令k=0,可得其中一条对称轴方程为x=$\frac{π}{6}$,
故选:B.
点评 本题主要考查两角和差的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:选择题
 如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )| A. | $\frac{20π}{3}$ | B. | 8π | C. | 9π | D. | $\frac{19π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
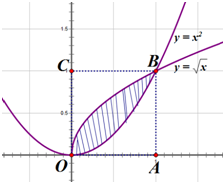 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温x (℃) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com