
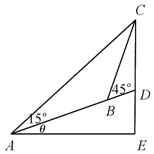
 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值. 分析 在△ABC中,根据正弦定理求出BC,在△BCD中,推出∠CDB=90°+θ,通过正弦定理转化求解即可.
解答 解:在△ABC中,∠BAC=15°,AB=100米,
∠ACB=45°-15°=30°. (3分)
根据正弦定理有$\frac{100}{sin30°}$=$\frac{BC}{sin15°}$,
∴BC=$\frac{100sin15°}{sin30°}$. (6分)
又在△BCD中,∵CD=50,BC=$\frac{100sin15°}{sin30°}$,∠CBD=45°,∠CDB=90°+θ,
根据正弦定理有$\frac{50}{sin45°}$=$\frac{\frac{100sin15°}{sin30°}}{sin(90°+θ)}$. (10分)
解得cosθ=$\sqrt{3}$-1 (12分)
点评 本题考查正弦定理的实际应用,解三角形的方法,考查计算能力.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{7}{10})$ | B. | $(-∞,-\frac{4}{5})$ | C. | $(-\frac{63}{80},+∞)$ | D. | $(-\frac{40}{49},-\frac{4}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
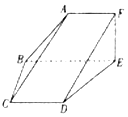 如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.
如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com