练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知函数f（x）=log3x，x0∈[1，27]，则不等式1≤f（x0）≤2成立的概率是（　　）
    A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{3}{13}$D．$\frac{2}{9}$

    分析 计算出满足不等式1≤f（x0）≤2成立的x的范围，根据区间的长度之比求出概率即可．

    解答 解：由log33=1，log39=2，
    故不等式1≤f（x0）≤2成立的概率p=$\frac{9-3}{27-1}$=$\frac{3}{13}$，
    故选：C．

    点评 本题考查了对数函数的性质，考查几何概型问题，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．已知抛物线y2=16x的焦点恰好是双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点，则双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\frac{1}{3}$x3-mx2+x+2有两个极值点，则m的取值范围是（　　）
    A．（-1，1）B．[-1，1]C．（-∞，-1]∪[1，+∞）D．（-∞，-1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知各项均为正数的等比数列{an}的前n项和为Sn，若a5=2a3+a4，且S5=62．
    （1）求数列{an}的通项公式；
    （2）设bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$，数列{bn}的前n项和为Tn，求证：$\frac{1}{3}$≤Tn＜$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=x2-x|x-a|-3a，a＞0．
    （1）若a=1，求f（x）的单调区间；
    （2）求函数在x∈[0，3]上的最值；
    （3）当a∈（0，3）时，若函数f（x）恰有两个不同的零点x1，x2，求$|{\frac{1}{x_1}-\frac{1}{x_2}}|$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某校高三共有2000名学生参加广安市联考，现随机抽取100名学生的成绩单（单位：分），并列成如表所示的频数分布表：
    组别[40，50）[50，60）[60，70）[70，80）[80，90）[90，100]
    频数6182826175
    （1）试估计该年级成绩≥80分的学生人数；
    （2）已知样本在成绩在[40，50）中的6名学生中，有4名男生，2名女生，现从中选2人进行调研，求恰好选中一名男生一名女生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知抛物线C：y2=-4x的焦点为F，A（-2，1），P为抛物线C上的动点，则|PF|+|PA|的最小值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知直线l过点（0，5），且在两坐标轴上的截距之和为2．
    （1）求直线l的方程；
    （2）若直线l1过点（$\frac{8}{3}$，-1）且与直线l垂直，直线l2与直线l1关于x轴对称，求直线l2的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

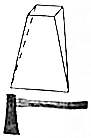    13．斧头的形状叫楔形，在《算数书》中又称之为“郓（y$\stackrel{、}{u}$n）都”或“壍（qi$\stackrel{、}{a}$n）堵”：其上底是一矩形，下底是一线段．有一斧头：上厚为三，下厚为六，高为五及袤（m$\stackrel{、}{a}$o）为二，问此斧头的体积为几何？意思就是说有一斧头形的几何体，上底为矩形，下底为一线段，上底的长为3，下底线段长为6，上下底间的距离（高）为5，上底矩形的宽为2，则此几何体的体积是（　　）
    A．6B．10C．16D．20

    查看答案和解析>>

    同步练习册答案