
已知函数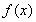 的定义域为
的定义域为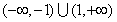 ,对定义域内的任意x,满足
,对定义域内的任意x,满足 ,当
,当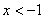 时,
时,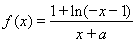 (a为常),且
(a为常),且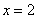 是函数
是函数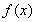 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当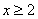 时,不等式
时,不等式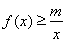 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: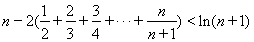
(1)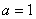 ;(2)2;(3)详见解析.
;(2)2;(3)详见解析.
【解析】
试题分析:(1)利用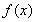 为奇函数,所以设
为奇函数,所以设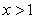 ,利用
,利用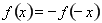 ,求出
,求出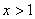 时的
时的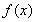 ,然后再求
,然后再求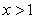 时的
时的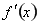 ,再根据
,再根据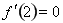 ,求出
,求出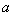 ,验证所求
,验证所求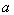 能够使
能够使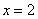 是函数
是函数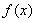 的一个极值点;(2)不等式
的一个极值点;(2)不等式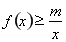 恒成立,转化为
恒成立,转化为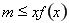 恒成立,设
恒成立,设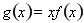 ,即求
,即求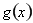 的最小值,求
的最小值,求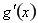
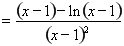 ,再设
,再设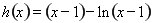 ,易求
,易求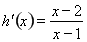 ,当
,当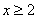 时,
时,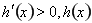 为增函数,
为增函数,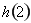 最小,
最小,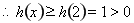 ,即
,即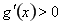 逐步分析
逐步分析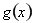 为单调递增函数,从而求得最小值.(3)通过
为单调递增函数,从而求得最小值.(3)通过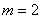 代入(2)式恒成立不等式
代入(2)式恒成立不等式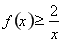 ,变形放缩后得到
,变形放缩后得到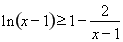 ,为出现(2)要证形式,所以令
,为出现(2)要证形式,所以令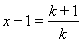 ,则
,则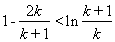 ,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
试题解析:(1)由题知对定义域内任意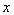 ,
,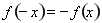 ,
,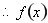 为奇函数,
为奇函数,
当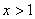 时,
时,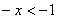 ,
,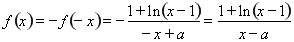 ,
,
当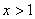 时,
时,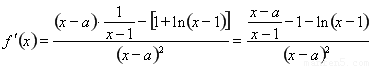
由题知: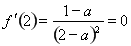 ,解得
,解得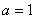 ,经验证,满足题意.
,经验证,满足题意.
(2)由(1)知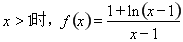
当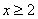 时,
时,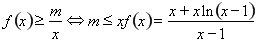 ,令
,令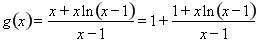
则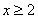 时,
时,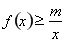 恒成立,转化为
恒成立,转化为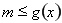 在
在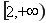 恒成立.
恒成立.
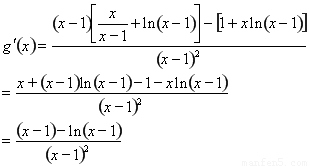
令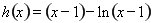 ,
,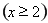 ,则
,则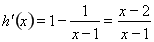 ,
,
当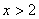 时,
时,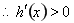 ,
,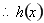 在
在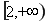 上单调递增.
上单调递增.
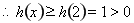
 当
当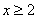 时,
时,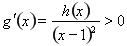 ,
,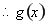 在
在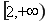 单调递增.
单调递增.
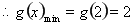
则若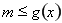 在
在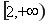 恒成立,则
恒成立,则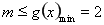
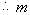 的最大值2.
的最大值2.
(3)由(2)知当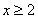 时,有
时,有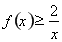 ,即
,即
则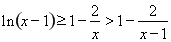
令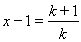 ,则
,则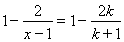
 当
当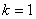 时,
时,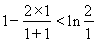 ;当
;当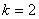 时,
时,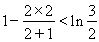 ;当
;当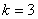 时,
时,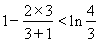 ;
;
当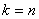 时,
时,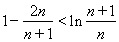
 将以上不等式两端分别相加得:
将以上不等式两端分别相加得:
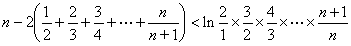
即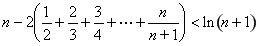 .
.
考点:1.函数极值的应用;2.利用导数求最值;3.证明不等式的方法.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省杭州市七校高三上学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数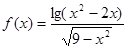 的定义域为
的定义域为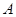 ,
,
(1)求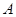 ;
;
(2)若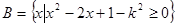 ,且
,且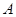 是
是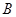 的真子集,求实数
的真子集,求实数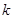 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届辽宁朝阳高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知函数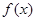 的定义域为
的定义域为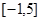 ,部分对应值如下表。
,部分对应值如下表。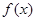 的导函数
的导函数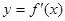 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数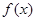 的命题:
的命题:
①函数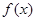 在
在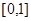 上是减函数;②如果当
上是减函数;②如果当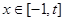 时,
时,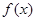 最大值是
最大值是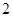 ,那么
,那么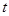 的最大值为
的最大值为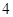 ;③函数
;③函数 有
有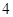 个零点,则
个零点,则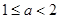 ;④已知
;④已知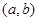 是
是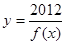 的一个单调递减区间,则
的一个单调递减区间,则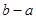 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省海口市高三高考调研考试理科数学 题型:选择题
已知函数 的定义域为
的定义域为 ,且
,且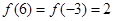 ,
,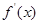 为
为 的导函数,函数
的导函数,函数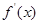 的图象如图所示.若正数
的图象如图所示.若正数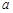 ,
,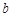 满足
满足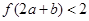 ,则
,则 的取值范围是
的取值范围是
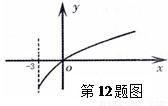
A. 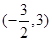 B.
B.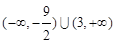 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com