
【题目】已知圆![]() 的方程为
的方程为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线
相切的直线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
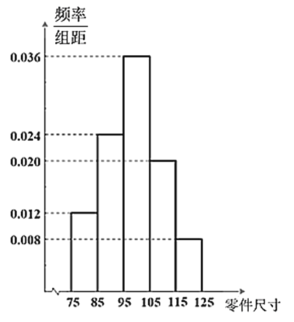
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l过点![]() .
.
(1)若直线l的纵截距和横截距相等,求直线l的方程;
(2)若直线l与两坐标轴围成的三角形的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
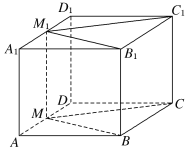
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.
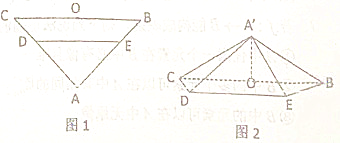
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意![]() 都有
都有![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() ,给出如下命题:
,给出如下命题:
①![]() ;
;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com