
【题目】已知a,b,c为正实数,且满足a+b+c=1.证明:
(1)|a![]() |+|b+c﹣1|
|+|b+c﹣1|![]() ;
;
(2)(a3+b3+c3)(![]() )≥3.
)≥3.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据a,b,c为正实数,且满足a+b+c=1,得到b+c﹣1=﹣a<0,则|a![]() |+|b+c﹣1|=|a
|+|b+c﹣1|=|a![]() |+|﹣a|,再利用绝对值三角不等式求解.
|+|﹣a|,再利用绝对值三角不等式求解.
(2)利用(a3+b3+c3)≥3abc,得到(a3+b3+c3)(![]() )≥3abc(
)≥3abc(![]() ),进而变形为
),进而变形为![]() ,再利用基本不等式求解.
,再利用基本不等式求解.
(1)∵a,b,c为正实数,且满足a+b+c=1,
∴b+c﹣1=﹣a<0,
∴|a![]() |+|b+c﹣1|=|a
|+|b+c﹣1|=|a![]() |+|﹣a|≥|(a
|+|﹣a|≥|(a![]() )+(﹣a)|
)+(﹣a)|![]() .
.
当且仅当(a![]() )(﹣a)≥0,即0
)(﹣a)≥0,即0![]() 时,等号成立.
时,等号成立.
∴|a![]() |+|b+c﹣1|
|+|b+c﹣1|![]() ;
;
(2)(a3+b3+c3)(![]() )≥3abc
)≥3abc![]() ,
,
![]() ,
,
![]() ,
,
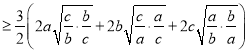 ,
,
=3(a+b+c)=3.
当且仅当a=b=c![]() 时等号成立.
时等号成立.
∴(a3+b3+c3)(![]() )≥3.
)≥3.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
B.命题“存在![]() ,使得
,使得![]() ”的否定是:“对任意
”的否定是:“对任意![]() ,均有
,均有![]() ”
”
C.命题“角![]() 的终边在第一象限角,则
的终边在第一象限角,则![]() 是锐角”的逆否命题为真命题
是锐角”的逆否命题为真命题
D.已知![]() 是
是![]() 上的可导函数,则“
上的可导函数,则“![]() ”是“
”是“![]() 是函数
是函数![]() 的极值点”的必要不充分条件
的极值点”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国家为了鼓励高校毕业生自主创业,出台了许多优惠政策,以创业带动就业.某高校毕业生小张自主创业从事苹果的种植,并开设网店进行销售.为了做好苹果的品控,小张从自己果园的苹果树上,随机摘取150个苹果测重(单位:克),其重量分布在区间![]() 内,根据统计的数据得到如图1所示的频率分布直方图.
内,根据统计的数据得到如图1所示的频率分布直方图.
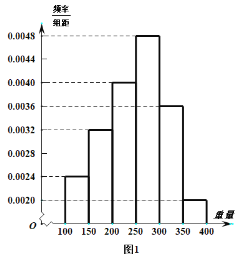
(1)以上述样本数据中频率作为概率,现一顾客从该果园购买了30个苹果,求这30个苹果中重量在![]() 内的个数
内的个数![]() 的数学期望;
的数学期望;
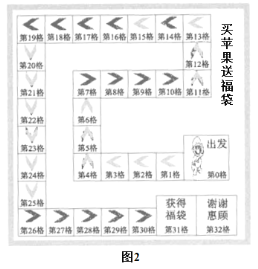
(2)小张的网店为了进行苹果的促销,推出了“买苹果,送福袋”的活动,买家在线参加按图行进赢取福袋的游戏.该游戏的规则如下:买家点击抛掷一枚特殊的骰子,每次抛掷的结果为1或2,且这两种结果的概率相同;从出发格(第0格)开始,每掷一次,按照抛掷的结果,按如图2所示的路径向前行进一次,若掷出1点,即从当前位置向前行进一格(从第![]() 格到第
格到第![]() 格,
格,![]() ),若掷出2点,即从当前位置向前行进两格(从第
),若掷出2点,即从当前位置向前行进两格(从第![]() 格到第
格到第![]() 格,
格,![]() ),行进至第3l格(获得福袋)或第32格(谢谢惠顾),游戏结束.设买家行进至第
),行进至第3l格(获得福袋)或第32格(谢谢惠顾),游戏结束.设买家行进至第![]() 格的概率为
格的概率为![]() ,
,![]() .
.
(ⅰ)求![]() 、
、![]() ,并写出用
,并写出用![]() 、
、![]() 表示
表示![]() 的递推式;
的递推式;
(ⅱ)求![]() ,并说明该大学生网店推出的此款游戏活动,是更有利于卖家,还是更有利于买家.
,并说明该大学生网店推出的此款游戏活动,是更有利于卖家,还是更有利于买家.
查看答案和解析>>
科目:高中数学 来源: 题型:
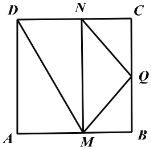
【题目】如图,在边长等于2正方形![]() 中,点Q是
中,点Q是![]() 中点,点M,N分别在线段
中点,点M,N分别在线段![]() 上移动(M不与A,B重合,N不与C,D重合),且
上移动(M不与A,B重合,N不与C,D重合),且![]() ,沿着
,沿着![]() 将四边形
将四边形![]() 折起,使得二面角
折起,使得二面角![]() 为直二面角,则三棱锥
为直二面角,则三棱锥![]() 体积的最大值为________;当三棱锥
体积的最大值为________;当三棱锥![]() 体积最大时,其外接球的表面积为________.
体积最大时,其外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为1的等差数列,
是公差为1的等差数列,![]() 是单调递增的等比数列,且
是单调递增的等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ;
;
(3)若数列![]() 的前
的前![]() 项积为
项积为![]() ,求
,求![]() .
.
(4)数列![]() 满足
满足![]() ,
,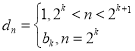 ,其中
,其中![]() ,
,![]() ,求
,求![]() .
.
(5)解决数列问题时,经常需要先研究陌生的通项公式,只有先把通项公式研究明白,然后尽可能转化为我们熟悉的数列问题,由此使问题得到解决.通过对上面(2)(3)(4)问题的解决,你认为研究陌生数列的通项问题有哪些常用方法,要求介绍两个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 做
做![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
①求证:![]() ;
;
②记四边形![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,若
,若![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com