已知数{an}的前n项和为Sn,且满Sn=2an-n(n=1,2,3_)
(1)a1,a2,a3的值;
(2)求证:数列{an+1}是等比数列;
(3)bn=nan,求数{bn}的前n项Tn.
【答案】
分析:(1)分别令n=1,2,3代入,计算可得数列的值;
(2)由S
n=2a
n-n,可得S
n-1=2a
n-1-(n-1),两式相减易得;
(3)由(2)可得b
n=n•2
n-n,分别由错位相减法和等差数列的求和公式可得答案.
解答:解:(1)因为S
n=2a
n-n,令n=1,解得a
1=1,
分别再令n=2,n=3,可解得a
2=3,a
3=7;
(2)因为n>1,n∈N),
两式相减可得a
n=2a
n-1+1,即a
n+1=2(a
n-1+1),
又a
1+1=2,所以{a
n+1}构成首项为2,公比为2的等比数列;
(3)因为{a
n+1}构成首项为2,公比为2的等比数列,
所以
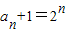
,所以a
n=2
n-1,
因为b
n=na
n,所以b
n=n•2
n-n,
所以T
n=1•2
1+2•2
2+3•2
3+…+(n-1)•2
n-1+n•2
n-(1+2+3+…+n),
令H
n=1•2
1+2•2
2+3•2
3+…+(n-1)•2
n-1+n•2
n (1)
则2H
n=1•2
2+2•2
3+3•2
4+…+(n-1)•2
n+n•2
n+1 (2)
(1)-(2)得:-H
n=2
1+2
2+2
3+…+2
n-n•2
n+1=
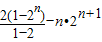
=(1-n)•2
n+1-2,故H
n=2+(n-1)•2
n+1,
所以T
n=2+(n-1)•2
n+1-
 点评:
点评:本题考查数列的求和,涉及等比关系的确定和错位相减法求和,属中档题.

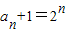 ,所以an=2n-1,
,所以an=2n-1,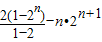 =(1-n)•2n+1-2,故Hn=2+(n-1)•2n+1,
=(1-n)•2n+1-2,故Hn=2+(n-1)•2n+1,

