
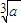 (a>0),由递推公式xn+1=
(a>0),由递推公式xn+1= (xn+
(xn+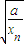 )(n∈N)得到数列{xn},对于任意的n∈N,都有xn>
)(n∈N)得到数列{xn},对于任意的n∈N,都有xn>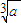 ,用数列{xn}可以计算
,用数列{xn}可以计算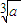 的近似值.
的近似值. (xn-1-xn);
(xn-1-xn);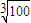 的近似值,要求|xn-xn+1|<10-4,请你估计n,并说明理由.
的近似值,要求|xn-xn+1|<10-4,请你估计n,并说明理由.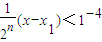 ,由此可估计n的值.
,由此可估计n的值. (xn+
(xn+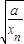 )
) (5+
(5+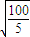 )≈4.74
)≈4.74 (xn-1-xn)=
(xn-1-xn)=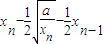 =
=
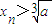 ;
;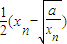 =
=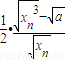 >0
>0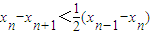 ;
;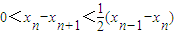 <…<
<…<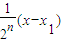
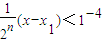 ,即2n>104(x-x1)
,即2n>104(x-x1)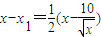
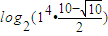 =15.1
=15.1

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com