【题目】如图，已知三棱锥
，点
是
的中点，且
，
，过点作一个截面，使截面平行于
和
，则截面的周长为（ ）
A.
B.
C.
D.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某公司计划购买2台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记
表示2台机器三年内共需更换的易损零件数，
表示购买2台机器的同时购买的易损零件数.
（Ⅰ）求的分布列；
（Ⅱ）若要求
，确定的最小值；
（Ⅲ）以购买易损零件所需费用的期望值为决策依据，在
与
之中选其一，应选用哪个？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动，有Ⅳ人参加，现将所有参加者按年龄情况分为
，
，
，
，
，
，
等七组，其频率分布直方图如图所示，已知这组的参加者是6人．
（1）根据此频率分布直方图求该校参加秋季登山活动的教职工年龄的中位数；
（2）已知和这两组各有2名数学教师，现从这两个组中各选取2人担任接待工作，设两组的选择互不影响，求两组选出的人中恰有1名数学老师的概率；
（3）组织者从
这组的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为
，求的分布列和均值．
查看答案和解析>>
科目：高中数学 来源： 题型：
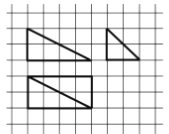
【题目】我国古代数学名著《九章算术·商功》中阐述：“斜解立方，得两壍堵。斜解壍堵，其一为阳马，一为鳖臑.阳马居二，鳖臑居一，不易之率也.合两鳖臑三而一，验之以棊，其形露矣.”若称为“阳马”的某几何体的三视图如图所示，图中网格纸上小正方形的边长为1，则对该几何体描述：
①四个侧面都是直角三角形；
②最长的侧棱长为
；
③四个侧面中有三个侧面是全等的直角三角形；
④外接球的表面积为
.
其中正确的个数为（ ）
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“科技引领，布局未来”科技研发是企业发展的驱动力量。
年，某企业连续
年累计研发投入搭
亿元，我们将研发投入与经营投入的比值记为研发投入占营收比，这年间的研发投入（单位：十亿元）用右图中的折现图表示，根据折线图和条形图，下列结论错误的使（ ）
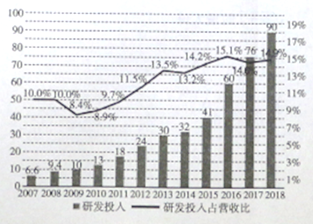
A. 
年至
年研发投入占营收比增量相比
年至
年增量大
B. 年至
年研发投入增量相比
年至
年增量小
C. 该企业连续年研发投入逐年增加
D. 该企业来连续年来研发投入占营收比逐年增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，椭圆
离心率为
，
、
是椭圆C的短轴端点，且到焦点的距离为
，点M在椭圆C上运动，且点M不与、重合，点N满足
．
（1）求椭圆C的方程；
（2）求四边形
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，满足acosB+bcosA=2ccosC．
（1）求角C的大小；
（2）若△ABC的周长为3，求△ABC的内切圆面积S的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，已知曲线
（
为参数），
.以原点
为极点，
轴的非负半轴为极轴建立极坐标系.
（I）写出曲线
与圆
的极坐标方程；
（II）在极坐标系中，已知射线
分别与曲线及圆相交于
，当
时，求
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
