
【题目】已知{an}是递增的等差数列a3= ![]() ,且a2a4=6.
,且a2a4=6.
(1)求{an}的首项a1和公差d;
(2)求{an}的通项和前n项和Sn .
【答案】
(1)解:由题意得公差d>0,
a3= ![]() ,且a2a4=6,
,且a2a4=6,
可得a2+a4=2a3=5,
解得a2=2,a4=3,
可得2d=a4﹣a2=1,解得d= ![]() ,
,
则a1=a2﹣d= ![]() ;
;
(2)解:{an}的通项an=a1+(n﹣1)d= ![]() +
+ ![]() (n﹣1)=
(n﹣1)= ![]() (n+2);
(n+2);
前n项和Sn=na1+ ![]() n(n﹣1)d=
n(n﹣1)d= ![]() n+
n+ ![]() n(n﹣1)=
n(n﹣1)= ![]() n2+
n2+ ![]() n.
n.
【解析】(1)由题意得公差d>0,运用等差数列中项的性质,解方程可得a2=2,a4=3,运用等差数列的通项公式可得公差d和首项;(2)运用等差数列的通项公式和求和公式,化简计算即可得到所求.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系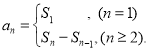 才能正确解答此题.
才能正确解答此题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,长轴长为4.
,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1 , y1),B(x2 , y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.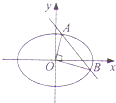
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( ) 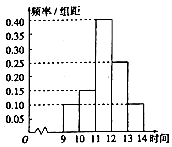
A.100万元
B.10万元
C.7.5万元
D.6.25万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
A.3, ![]()
B.3, ![]()
C.4, ![]()
D.4, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com