【题目】已知函数
，
.
(I)若
恒成立，求实数
的取值范围；
(Ⅱ)当取(I)中的最小值时，求证: 
.
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案科目：高中数学 来源： 题型：
【题目】有关命题的说法错误的是（ ）
A.若p∨q为假命题，则p、q均为假命题
B.“x＝1”是“x2﹣3x+2＝0”的充分不必要条件
C.命题“若x2﹣3x+2＝0，则x＝1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”
D.对于命题p：x≥0，2x＝3，则￢P：x＜0，2x≠3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，某地出土的一种“钉”是由四条线段组成，其结构能使它任意抛至水平面后，总有一端所在的直线竖直向上．并记组成该“钉”的四条等长的线段公共点为
，钉尖为
．
（1）判断四面体
的形状，并说明理由；
（2）设
，当
在同一水平面内时，求
与平面
所成角的大小（结果用反三角函数值表示）；
（3）若该“钉”着地后的四个线段根据需要可以调节与底面成角的大小，且保持三个线段与底面成角相同，若
，，问
为何值时，
的体积最大，并求出最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题共
分）
若
或
，则称
为
和
的一个
位排列，对于，将排列
记为
，将排列
记为
，依此类推，直至
，对于排列和
，它们对应位置数字相同的个数减去对应位置数字不同的数，叫做和
的相关值，记作
，例如
，则
，
，若
，则称为最佳排列．
（Ⅰ）写出所有的最佳排列
．
（Ⅱ）证明：不存在最佳排列
．
（Ⅲ）若某个
（
是正整数）为最佳排列，求排列中的个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，
.
（1）当
时，若
在区间
上单调递减，求a的取值范围；
（2）求满足下列条件的所有实数对
：当a是整数时，存在
，使得
是的最大值，
是
的最小值；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C1：
，曲线C2：
．
（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；
（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线
，
．写出，的参数方程．与公共点的个数和C1与C2公共点的个数是否相同？说明你的理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】写出下列各组命题构成的“
或
”、“且”以及“非”形式的命题，并判断它们的真假．
(1)：
是有理数，：是整数；
(2)：不等式
的解集是
，：不等式的解集是
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】 (1)已知正数a，b满足a＋b＝1，求证：a2＋b2≥
；
(2)设a、b、c为△ABC的三条边，求证：a2＋b2＋c2<2(ab＋bc＋ca)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高中学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[50,100]内，发布成绩使用等级制．各等级划分标准见图表．规定：A，B，C三级为合格等级，D为不合格等级.
分数 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．按照[50,60)，[60,70)，[70,80)，[80,90)，[90,100]的分组作出频率分布直方图如图①所示，样本中原始成绩在80分及以上的所有数据的茎叶图如图②所示．
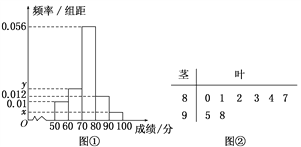
(1)求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；
(2)在选取的样本中，从成绩为A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生的成绩是A等级的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
