
分析 由指数函数的图象和性质,可判断①;由直线与平面位置关系的几何特征,可判断②;根据椭圆的定义,可判断③;根据双曲线的简单性质,可判断④.
解答 解:①命题“每个指数函数都是单调函数”可化为:“?函数f(x)=ax,(a>0,且a≠1),f(x)为单调函数”,是全称命题,而且是真命题,故正确;
②若m?α,n?α,m,n是异面直线,那么n与α相交,或n与α平行,故错误;
③设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=2a(a>3),则动点P的轨迹是椭圆,故错误;
④若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的焦点均为(±$\sqrt{34-k}$,0),故正确;
故答案为:①④
点评 本题以命题的真假判断与应用为载体,考查了指数函数的图象和性质,直线与平面位置关系,圆锥曲线的定义和性质,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.
如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {-2,-1,1,2,4} | C. | {1,4} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<4} | B. | {x|1<x<7} | C. | {x|1<x<4} | D. | {x|4<x<7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
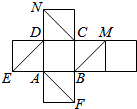 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com