
【题目】设A,B是非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合中B都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射,设f:x→ ![]() 是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B=;②若B={1,2},则A∩B= .
是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B=;②若B={1,2},则A∩B= .
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log ![]() (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x﹣14y+45=0及点Q(﹣2,3).
(1)若M为圆C上任一点,求|MQ|的最大值和最小值;
(2)若实数m,n满足m2+n2﹣4m﹣14n+45=0,求k= ![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法:
①垂直于同一平面的所有向量一定共面;
②在△ABC中,已知 ![]() ,则∠A=60°;
,则∠A=60°;
③在△ABC中,sin2A=sin2B+sin2C+sinBsinC,则A= ![]()
④若a>0,b>0,a+b=2,则a2+b2≥2;
正确的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞某家具生产厂家根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产书桌、书柜、电脑椅共120张,且书桌至少生产20张.已知生产这些家具每张所需工时和每张产值如表:
家具名称 | 书桌 | 书柜 | 电脑椅 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产书桌、书柜、电脑椅各多少张,才能使产值最高?最高产值是多少?(以千元为单位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( ) 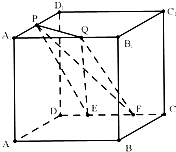
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定点M(3, ![]() )与抛物线y2=2x上的点P的距离为d1 , P到抛物线准线l的距离为d2 , 则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1 , P到抛物线准线l的距离为d2 , 则d1+d2取最小值时,P点的坐标为( )
A.(0,0)
B.(1, ![]() )
)
C.(2,2)
D.( ![]() ,-
,- ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com