
【题目】在底面是边长为6的正方形的四棱锥P--ABCD中,点P在底面的射影H为正方形ABCD的中心,异面直线PB与AD所成角的正切值为![]() ,则四棱锥P--ABCD的内切球与外接球的半径之比为( )
,则四棱锥P--ABCD的内切球与外接球的半径之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
确定异面直线PB与AD所成角为∠PBC,取BC中点E,则tan∠PBC![]() ,求出PE=5,HP=4,可得四棱锥P﹣ABCD的表面积、体积,进而求出内切球的半径,利用勾股定理求出外接球的半径,即可求出四棱锥P﹣ABCD的内切球与外接球的半径之比.
,求出PE=5,HP=4,可得四棱锥P﹣ABCD的表面积、体积,进而求出内切球的半径,利用勾股定理求出外接球的半径,即可求出四棱锥P﹣ABCD的内切球与外接球的半径之比.
由题意,四棱锥P﹣ABCD为正四棱锥,PA=PB=PC=PD,
∵AD∥BC,
∴异面直线PB与AD所成角为∠PBC,
取BC中点E,则tan∠PBC![]() ,
,
∴PE=5,HP=4,
从而四棱锥P﹣ABCD的表面积为S![]() 96,V
96,V![]() 48,
48,
∴内切球的半径为r![]() .
.
设四棱锥P﹣ABCD外接球的球心为O,外接球的半径为R,则OP=OA,
∴(4﹣R)2+(3![]() )2=R2,
)2=R2,
∴R![]() ,
,
∴![]() .
.
故选D.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC—A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AC=AA1=2,点M,N分別为A1B和B1C1的中点.
(1)求异面直线A1B与NC所成角的余弦值;
(2)求A1B与平面NMC所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为2的正三角形ABC中,点D,E,G分别是边AB,AC,BC的中点,连接DE,连接AG交DE于点![]() 现将
现将![]() 沿DE折叠至
沿DE折叠至![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED,连接A1G,EG.
平面BCED,连接A1G,EG.
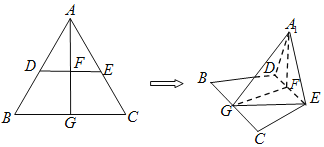
![]() 证明:DE∥平面A1BC
证明:DE∥平面A1BC
![]() 求点B到平面A1EG的距离.
求点B到平面A1EG的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() ).
).
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)若![]() ,试判断
,试判断![]() 的上单调性,并证明你的结论;
的上单调性,并证明你的结论;
(3)是否存在![]() ,使得当
,使得当![]() 时,
时, ![]() 有最大值
有最大值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com