
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,底面
的中点,底面![]() 是正三角形,延长
是正三角形,延长![]() 到点
到点![]() ,使得
,使得![]() .
.
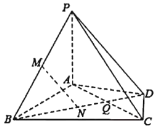
(1)![]() 为线段
为线段![]() 上确定一点,当
上确定一点,当![]() 平面
平面![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 平面
平面![]() ,且
,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
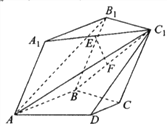
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,
,![]() 的面积为2.
的面积为2.
(I)求椭圆C的方程;
(II)设M是椭圆C上一点,且不与顶点重合,若直线![]() 与直线
与直线![]() 交于点P,直线
交于点P,直线![]() 与直线
与直线![]() 交于点Q.求证:△BPQ为等腰三角形.
交于点Q.求证:△BPQ为等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() 满足
满足![]() 是
是![]() 上的单调函数,且
上的单调函数,且![]() 在区间
在区间![]() 上的值域也为
上的值域也为![]() ,则称函数
,则称函数![]() 为区间
为区间![]() 上的“保值函数”,
上的“保值函数”,![]() 为“保值区间”.根据此定义给出下列命题:①函数
为“保值区间”.根据此定义给出下列命题:①函数![]() 是
是![]() 上的“保值函数”;②若函数
上的“保值函数”;②若函数![]() 是
是![]() 上的“保值函数”,则
上的“保值函数”,则![]() ;③对于函数
;③对于函数![]() 存在区间
存在区间![]() ,且
,且![]() ,使函数
,使函数![]() 为
为![]() 上的“保值函数”.其中所有真命题的序号为( )
上的“保值函数”.其中所有真命题的序号为( )
A.②B.③C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x+2|,g(x)=|x+2|﹣|x﹣2a|+a.
(1)求不等式f(x)>4的解集;
(2)对x1∈R,x2∈R,使得f(x1)≥g(x2)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() (a>b>0)过点E(
(a>b>0)过点E(![]() ,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(
,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(![]() ,0).
,0).
(1)求椭圆C的方程:
(2)设M(x0,y0)为椭圆C上异于A,B两点的任意一点,MN⊥AB于点N,直线l:x0x+2y0y﹣4=0,设过点A与x轴垂直的直线与直线l交于点P,证明:直线BP经过线段MN的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com