
(БОаЁЬтТњЗж12Зж)
ЮЊСЫНтФГЩчЧјМвЭЅЕФдТОљгУЫЎСПЃЈЕЅЮЛЃКЖжЃЉЃЌЯжДгИУЩчЧјЫцЛњГщВщ ЛЇЃЌЛёЕУУПЛЇФГФъЕФдТОљгУЫЎСПЃЌВЂжЦзїСЫЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃЈШчЭМЃЉ.
ЛЇЃЌЛёЕУУПЛЇФГФъЕФдТОљгУЫЎСПЃЌВЂжЦзїСЫЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃЈШчЭМЃЉ.
ЃЈЂёЃЉЗжБ№ЧѓГіЦЕТЪЗжВМБэжа ЕФжЕЃЌВЂЙРМЦИУЩчЧјМвЭЅдТОљгУЫЎСПВЛГЌЙ§
ЕФжЕЃЌВЂЙРМЦИУЩчЧјМвЭЅдТОљгУЫЎСПВЛГЌЙ§ ЖжЕФЦЕТЪЃЛ
ЖжЕФЦЕТЪЃЛ
ЃЈЂђЃЉЩш ЁЂ
ЁЂ ЁЂ
ЁЂ ЪЧЛЇдТОљгУЫЎСПЮЊ
ЪЧЛЇдТОљгУЫЎСПЮЊ ЕФОгУёДњБэЃЌ
ЕФОгУёДњБэЃЌ ЁЂ
ЁЂ ЪЧЛЇдТОљгУЫЎСПЮЊ
ЪЧЛЇдТОљгУЫЎСПЮЊ ЕФОгУёДњБэ. ЯжДгетЮхЮЛОгУёДњБэжаШЮбЁСНШЫВЮМгЫЎМлТлжЄЛсЃЌЧыСаОйГіЫљгаВЛЭЌЕФбЁЗЈЃЌВЂЧѓОгУёДњБэ
ЕФОгУёДњБэ. ЯжДгетЮхЮЛОгУёДњБэжаШЮбЁСНШЫВЮМгЫЎМлТлжЄЛсЃЌЧыСаОйГіЫљгаВЛЭЌЕФбЁЗЈЃЌВЂЧѓОгУёДњБэ ЁЂ
ЁЂ жСЩйгавЛШЫБЛбЁжаЕФИХТЪЃЎ
жСЩйгавЛШЫБЛбЁжаЕФИХТЪЃЎ

(1)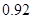 (2)
(2)
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКНтЃКЃЈЂёЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩЕУ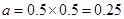 ЃЌЁЁЁЁЁ 2Зж
ЃЌЁЁЁЁЁ 2Зж
ЁрдТОљгУЫЎСПЮЊ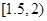 ЕФЦЕЪ§ЮЊ25.
ЕФЦЕЪ§ЮЊ25.
ЙЪ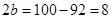 ЃЌЕУ
ЃЌЕУ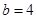 . ЁЁЁЁЁЁЁЁЁЁ
4Зж
. ЁЁЁЁЁЁЁЁЁЁ
4Зж
гЩЦЕТЪЗжВМБэПЩжЊЃЌЛЇдТОљгУЫЎСПВЛГЌЙ§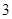 ЖжЕФЦЕТЪЮЊ
ЖжЕФЦЕТЪЮЊ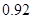 ЃЌ ЁЁЁ 5Зж
ЃЌ ЁЁЁ 5Зж
ИљОнбљБОЙРМЦзмЬхЕФЫМЯыЃЌЙРМЦИУЩчЧјМвЭЅдТОљгУЫЎСПВЛГЌЙ§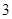 ЖжЕФЦЕТЪЮЊ
ЖжЕФЦЕТЪЮЊ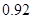 ЃЎ ЁЁЁ 6Зж
ЃЎ ЁЁЁ 6Зж
ЃЈЂђЃЉгЩ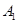 ЁЂ
ЁЂ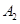 ЁЂ
ЁЂ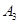 ЁЂ
ЁЂ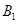 ЁЂ
ЁЂ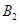 ЮхДњБэжаШЮбЁ
ЮхДњБэжаШЮбЁ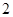 ШЫЙВгаШчЯТ
ШЫЙВгаШчЯТ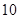 жжВЛЭЌбЁЗЈЃЌЗжБ№ЮЊЃК
жжВЛЭЌбЁЗЈЃЌЗжБ№ЮЊЃК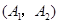 ЃЌ
ЃЌ ЃЌ
ЃЌ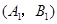 ЃЌ
ЃЌ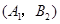 ЃЌ
ЃЌ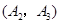 ЃЌ
ЃЌ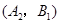 ЃЌ
ЃЌ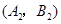 ЃЌ
ЃЌ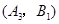 ЃЌ
ЃЌ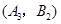 ЃЌ
ЃЌ . ЁЁЁЁЁЁЁЁЁЁ
8Зж
. ЁЁЁЁЁЁЁЁЁЁ
8Зж
МЧЁА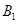 ЁЂ
ЁЂ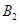 жСЩйгавЛШЫБЛбЁжаЁБЕФЪТМўЮЊ
жСЩйгавЛШЫБЛбЁжаЁБЕФЪТМўЮЊ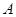 ЃЌЪТМў
ЃЌЪТМў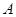 АќКЌЕФЛљБОЪТМўЮЊЃК
АќКЌЕФЛљБОЪТМўЮЊЃК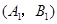 ЃЌ
ЃЌ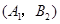 ЃЌ
ЃЌ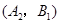 ЃЌ
ЃЌ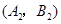 ЃЌ
ЃЌ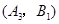 ЃЌ
ЃЌ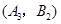 ЃЌ
ЃЌ ЃЌЙВАќКЌ7ИіЛљБОЪТМўЪ§. ЁЁЁЁЁЁ
10Зж
ЃЌЙВАќКЌ7ИіЛљБОЪТМўЪ§. ЁЁЁЁЁЁ
10Зж
гжЛљБОЪТМўЕФзмЪ§ЮЊ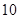 ЃЌЫљвд
ЃЌЫљвд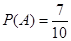 .
.
МДОгУёДњБэ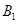 ЁЂ
ЁЂ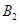 жСЩйгавЛШЫБЛбЁжаЕФИХТЪЮЊ
жСЩйгавЛШЫБЛбЁжаЕФИХТЪЮЊ . ЁЁЁЁЁЁЁЁ
12Зж
. ЁЁЁЁЁЁЁЁ
12Зж
ПМЕуЃКЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМ,ЙХЕфИХаЭ
ЕуЦРЃКФмНЋЪЕМЪЮЪЬтНсКЯЭГМЦКЭИХТЪЕФжЊЪЖРДЧѓНтЃЌПМВщСЫзЊЛЛгыЛЏЙщЫМЯыЕФдЫгУЃЌЛљДЁЧвживЊЃЌвЊЧѓеЦЮеКУЃЌВщЪ§ОнДІРэФмСІЁЂдЫЫуЧѓНтФмСІвдМАгІгУвтЪЖЃЌПМВщБиШЛгыЛђШЛЫМЯыЕШЪєгкжаЕЕЬтЁЃ


 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЃЈБОаЁЬтТњЗж12ЗжЃЉвбжЊКЏЪ§![]() ЃЌЧв
ЃЌЧв![]() ЁЃЂйЧѓ
ЁЃЂйЧѓ![]() ЕФзюДѓжЕМАзюаЁжЕЃЛЂкЧѓ
ЕФзюДѓжЕМАзюаЁжЕЃЛЂкЧѓ![]() ЕФдкЖЈвхгђЩЯЕФЕЅЕїЧјМф.
ЕФдкЖЈвхгђЩЯЕФЕЅЕїЧјМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЃЈ2009КўФЯОэЮФЃЉЃЈБОаЁЬтТњЗж12ЗжЃЉ
ЮЊРЖЏОМУдіГЄЃЌФГЪаОіЖЈаТНЈвЛХњжиЕуЙЄГЬЃЌЗжБ№ЮЊЛљДЁЩшЪЉЙЄГЬЁЂУёЩњЙЄГЬКЭВњвЕНЈЩшЙЄГЬШ§РрЃЌетШ§РрЙЄГЬЫљКЌЯюФПЕФИіЪ§ЗжБ№еМзмЪ§ЕФ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() .Яжга3УћЙЄШЫЖРСЂЕиДгжаШЮбЁвЛИіЯюФПВЮгыНЈЩш.ЧѓЃК
.Яжга3УћЙЄШЫЖРСЂЕиДгжаШЮбЁвЛИіЯюФПВЮгыНЈЩш.ЧѓЃК
ЃЈIЃЉЫћУЧбЁдёЕФЯюФПЫљЪєРрБ№ЛЅВЛЯрЭЌЕФИХТЪЃЛ w.w.w.k.s.5.u.c.o.m ![]()
![]()
ЃЈIIЃЉжСЩйга1ШЫбЁдёЕФЯюФПЪєгкУёЩњЙЄГЬЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЃЈБОаЁЬтТњЗж12ЗжЃЉ
ФГУёгЊЦѓвЕЩњВњAЃЌBСНжжВњЦЗЃЌИљОнЪаГЁЕїВщКЭдЄВтЃЌAВњЦЗЕФРћШѓгыЭЖзЪГЩе§БШЃЌЦфЙиЯЕШчЭМ1ЃЌBВњЦЗЕФРћШѓгыЭЖзЪЕФЫуЪѕЦНЗНИљГЩе§БШЃЌЦфЙиЯЕШчЭМ2ЃЌ
ЃЈзЂЃКРћШѓгыЭЖзЪЕЅЮЛЪЧЭђдЊЃЉ
ЃЈ1ЃЉЗжБ№НЋAЃЌBСНжжВњЦЗЕФРћШѓБэЪОЮЊЭЖзЪЕФКЏЪ§ЃЌВЂаДГіЫќУЧЕФКЏЪ§ЙиЯЕЪН.ЃЈ2ЃЉИУЦѓвЕвбГяМЏЕН10ЭђдЊзЪН№ЃЌВЂШЋВПЭЖШыЕНAЃЌBСНжжВњЦЗЕФЩњВњЃЌЮЪЃКдѕбљЗжХфет10ЭђдЊЭЖзЪЃЌВХФмЪЙЦѓвЕЛёЕУзюДѓРћШѓЃЌЦфзюДѓРћШѓЮЊЖрЩйЭђдЊ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com