60° (2,3]
分析:将已知的等式左右两边都乘以2变形后,利用正弦定理化简,再利用诱导公式及两角和与差的正弦函数公式变形,根据sinC不为0,得出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;由A的度数求出sinA的值,及B+C的度数,用B表示出C,由正弦定理表示出b与c,而三角形ABC的周长l=a+b+c,将表示出的b与c,及a的值代入,利用两角和与差的正弦函数公式化简,整理后再利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,由B的范围求出这个角的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即可得到l的范围.
解答:acosC+

c=b变形得:2acosC+c=2b,
利用正弦定理得:2sinAcosC+sinC=2sinB=2sin(A+C)=2sinAcosC+2cosAsinC,
∴sinC=2cosAsinC,即sinC(2cosA-1)=0,
由sinC≠0,得到cosA=

,
又A为三角形的内角,则A=60°;
∵a=1,sinA=

,B+C=120°,即C=120°-B,
∴

=

=

=

,即b=

sinB,c=

sin(120°-B),
则△ABC的周长l=a+b+c=1+

sinB+

sin(120°-B)
=1+

(

sinB+

cosB)
=1+2(

sinB+

cosB)
=1+2sin(B+30°),
∵0<B<120°,∴30°<B+30°<150°,
∴

<sin(B+30°)≤1,即2<1+2sin(B+30°)≤3,
则l范围为(2,3].
故答案为:60°;(2,3]
点评:此题考查了正弦定理,两角和与差的正弦函数公式,诱导公式,正弦函数的定义域与值域,以及特殊角的三角函数值,利用了转化的思想,熟练掌握定理及公式是解本题的关键.

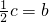 ,则角A的大小为________;若a=1,则△ABC的周长l的取值范围为________.
,则角A的大小为________;若a=1,则△ABC的周长l的取值范围为________. c=b变形得:2acosC+c=2b,
c=b变形得:2acosC+c=2b, ,
, ,B+C=120°,即C=120°-B,
,B+C=120°,即C=120°-B, =
= =
= =
= ,即b=
,即b= sinB,c=
sinB,c= sin(120°-B),
sin(120°-B), sinB+
sinB+ sin(120°-B)
sin(120°-B) (
( sinB+
sinB+ cosB)
cosB) sinB+
sinB+ cosB)
cosB) <sin(B+30°)≤1,即2<1+2sin(B+30°)≤3,
<sin(B+30°)≤1,即2<1+2sin(B+30°)≤3,

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案