将正整数2,3,4,5,6,7,…,n,…作如下分类:(2),(3,4),(5,6,7),(8,9,10,11),…,分别计算各组包含的正整数的和,记为S1,S2,S3,S4,…,记Tn=S1+S3+S5+…+S2n-1.
(1)分别求T1,T2,T3的值;
(2)请猜测Tn的结果,并用数学归纳法证明.
【答案】
分析:(1)第n组有n个从小到大连续的正整数,可求得第1个数是
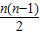
+2,利用等差数列的求和公式得S
n=
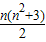
+2(n∈N
*),从而可求得S
1=2,S
3=18,S
5=70,继而可得T
1,T
2,T
3的值;
(2)猜想:T
n=n
2(n
2+1),(n∈N
*),利用数学归纳法证明即可,特别注意,假设当n=k(k∈N
*)时,猜测成立,即T
k=k
2(k
2+1)去推证n=k+1时等式也成立,要用好归纳假设.
解答:解:(1)第n组有n个从小到大连续的正整数,且第1个数是[1+2+3+…+(n-1)]+2=
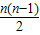
+2,
故S
n=n[
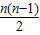
+2]+

=
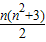
+2(n∈N
*).
S
1=2,S
3=18,S
5=70,T
1=S
1=2,
T
2=S
1+S
3=2+18=20,
T
3=S
1+S
3+S
5=2+18+70=90.…(6分)
(2)由(1)知T
1=2=1×2=1
2×(1
2+1),
T
2=20=4×5=2
2×(2
2+1),
T
3=90=9×10=3
2×(3
2+1)
猜想:T
n=n
2(n
2+1),(n∈N
*). …(10分)
证明:(ⅰ)当n=1时,已知成立.
(ⅱ)假设n=k(k∈N
*)时,猜测成立,即T
k=k
2(k
2+1).则n=k+1时,
T
k+1=T
k+S
2k+1=k
2(k
2+1)+
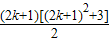
,
因为(k+1)
2[(k+1)
2+1]-k
2(k
2+1)-
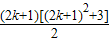
=[(k+1)
4-k
4]+[(k+1)
2-k
2]-
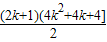
=[(k+1)
2+k
2][(k+1)
2-k
2]+(2k+1)-(2k+1)(2k
2+2k+2)
=(2k+1)(2k
2+2k+2)-(2k+1)(2k
2+2k+2)
=0,
所以k
2(k
2+1)+
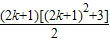
=(k+1)
2[(k+1)
2+1],即n=k+1时,猜测成立.
根据(ⅰ)(ⅱ),T
n=n
2(n
2+1)(n∈N
*)成立. …(16分)
点评:本题考查简单的合情推理,突出考查数学归纳法的应用,(1)中求得S
n=
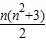
+2(n∈N
*)是难点,(2)猜想:T
n=n
2(n
2+1)(n∈N
*)是关键,考查运算与推理证明的能力,属于难题.

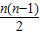 +2,利用等差数列的求和公式得Sn=
+2,利用等差数列的求和公式得Sn=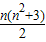 +2(n∈N*),从而可求得S1=2,S3=18,S5=70,继而可得T1,T2,T3的值;
+2(n∈N*),从而可求得S1=2,S3=18,S5=70,继而可得T1,T2,T3的值;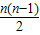 +2,
+2,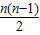 +2]+
+2]+ =
=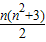 +2(n∈N*).
+2(n∈N*).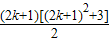 ,
,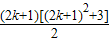
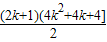
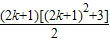 =(k+1)2[(k+1)2+1],即n=k+1时,猜测成立.
=(k+1)2[(k+1)2+1],即n=k+1时,猜测成立.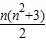 +2(n∈N*)是难点,(2)猜想:Tn=n2(n2+1)(n∈N*)是关键,考查运算与推理证明的能力,属于难题.
+2(n∈N*)是难点,(2)猜想:Tn=n2(n2+1)(n∈N*)是关键,考查运算与推理证明的能力,属于难题. 
