
【题目】已知圆![]() 的方程为:
的方程为:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 上有一动点
上有一动点![]() ,
,![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ,轨迹是一个焦点在
,轨迹是一个焦点在![]() 轴上的椭圆
轴上的椭圆
【解析】
(1)当直线![]() 垂直于
垂直于![]() 轴时,可验证其满足题意,得到直线方程为
轴时,可验证其满足题意,得到直线方程为![]() ;当直线
;当直线![]() 不垂直于
不垂直于![]() 轴时,设直线为
轴时,设直线为![]() ,利用垂径定理可求得圆心到直线距离
,利用垂径定理可求得圆心到直线距离![]() ,利用点到直线距离公式构造方程求得
,利用点到直线距离公式构造方程求得![]() ,从而得到直线方程;(2)设
,从而得到直线方程;(2)设![]() ,利用向量坐标运算可得到
,利用向量坐标运算可得到![]() ,
,![]() ,根据
,根据![]() 在圆
在圆![]() 上,可代入整理得到
上,可代入整理得到![]() 点轨迹.
点轨迹.
(1)当直线![]() 垂直于
垂直于![]() 轴时,此时直线方程为
轴时,此时直线方程为![]()
![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,这两点的距离为
,这两点的距离为![]() ,满足题意;
,满足题意;
当直线![]() 不垂直于
不垂直于![]() 轴时,设其方程为:
轴时,设其方程为:![]() ,即:
,即:![]()
设圆心到此直线的距离为![]() ,则:
,则:![]() ,解得:
,解得:![]()
![]() ,解得:
,解得:![]()
此时直线方程为:![]()
综上所述,所求直线方程为:![]() 或
或![]()
(2)设![]() 点的坐标为
点的坐标为![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
![]() ,
,![]()
∵![]() ∴
∴![]() ,即
,即![]()
∴![]() 点的轨迹方程是
点的轨迹方程是![]() ,轨迹是一个焦点在
,轨迹是一个焦点在![]() 轴上的椭圆
轴上的椭圆


科目:高中数学 来源: 题型:
【题目】某盒子内装有三种颜色的玻璃球,一位同学每次从中随机拿出一个玻璃球,观察颜色后再放回,重复了50次,得到的信息如下:观察到红色26次、蓝色13次.如果从这个盒子内任意取一个玻璃球,估计:
(1)这个球既不是红色也不是蓝色的概率;
(2)这个球是红色或者是蓝色的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
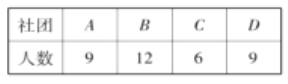
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
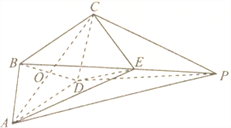
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com