
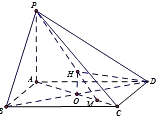
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠BAD=120°,对角线AC与BD交于点O,M为OC中点. 
(1)求证:BD⊥PM
(2)若二面角O﹣PM﹣D的正切值为2 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)证明:∵四棱锥P﹣ABCD中,PA⊥平面ABCD,
又BD平面ABCD,∴BD⊥PA,
∵底面ABCD是菱形,
∴BD⊥AC,
又PA∩AC=A,∴BD⊥平面PAC,
又PM平面PAC,
∴BD⊥PM.
(2)解:过O作OH⊥PM交PM于H,连HD,
因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,
所以∠OHD为A﹣PM﹣D的平面角,
设PA=b,AD=4,
∵底面ABCD是边长为4的菱形,∠BAD=120°,
∴OD=2 ![]() ,OM=1,AM=3,且
,OM=1,AM=3,且 ![]() =
= ![]() ,
,
从而OH= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠OHD= ![]() =
= ![]() ,
,
所以16b2=144,解得b=3.(舍负值)
∴PA的长为3.
则 ![]() =
= ![]() .
.
【解析】(1)根据线面垂直的判定,先证明BD⊥平面PAC,利用线面垂直的性质即可证明BD⊥PM.(2)过O作OH⊥PM交PM于H,连HD,则∠OHD为A﹣PM﹣D的平面角,利用二面角O﹣PM﹣D的正切值为2 ![]() ,即可求出
,即可求出 ![]() 的值.
的值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】现有4人去旅游,旅游地点有A,B两个地方可以选择,但4人都不知道去哪里玩,于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩,掷出能被3整除的数时去A地,掷出其他的则去B地.
(1)求这4个人恰好有1个人去A地的概率;
(2)用X,Y分别表示这4个人中去A,B两地的人数,记ξ=XY,求随机变量ξ的分布列与数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对新研发的一批产品进行合理定价,将产品按事先拟定的价格进行试销,得到一组销售数据![]() 2,
2,![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | 90 | 84 | 83 | 80 | q | 68 |
已知![]() .
.
![]() 求表格中q的值;
求表格中q的值;
![]() 已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程
已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程![]() 参考数据
参考数据![]() ;
;
![]() 用
用![]() 中的回归方程得到的与
中的回归方程得到的与![]() 对应的产品销量的估计值记为
对应的产品销量的估计值记为![]() 2,
2,![]() ,
,![]() 当
当![]() 时,则称
时,则称![]() 为一个“理想数据”
为一个“理想数据”![]() 试确定销售单价分别为4,5,6时有哪些是“理想数据”.
试确定销售单价分别为4,5,6时有哪些是“理想数据”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=x2﹣x+alnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证f(x2)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区规划时,计划在周边建造一片扇形绿地,如图所示已知扇形绿地的半径为50米,圆心角![]() 从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与
从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与![]() 均为直线段
均为直线段![]() ,其中PC平行于绿地的边界
,其中PC平行于绿地的边界![]() 记
记![]() 其中
其中![]()

![]() 当
当![]() 时,求所需铺设的道路长:
时,求所需铺设的道路长:
![]() 若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当
若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当![]() 变化时,求铺路所需费用的最大值
变化时,求铺路所需费用的最大值![]() 精确到1元
精确到1元![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:

用广告费作解释变量,年销售额作预报变量,若认为![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型,则
的回归方程类型,则
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知商品的年利润![]() 与
与![]() 的关系式为
的关系式为![]() .根据(1)的结果,年广告费
.根据(1)的结果,年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大?
约为何值时(小数点后保留两位),年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
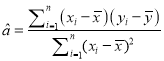 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,给出下列四个命题:①三棱锥
,给出下列四个命题:①三棱锥![]() 的体积为定值;②异面直线
的体积为定值;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③
;③![]() 平面
平面![]() ;④直线
;④直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .其中正确的命题为( )
.其中正确的命题为( )
A. ①② B. ②③ C. ①②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com