
 ij����ũׯ��һ�鳤��������ABCD��AB=100�ף�BC=50$\sqrt{3}$�ף�Ϊ�˱����ο�����ɢ������ũׯ�����������ڽ�3����ͼ��ʾ�Ĺ۹�����OE��EF��OF�����ǵ�����滮��Ҫ��O��AB���е㣬��E�ڱ�BC�ϣ���F�ڱ�AD�ϣ��������㣩���ҡ�EOF=90�㣮��$\sqrt{2}$��1.4��$\sqrt{3}$��1.7��
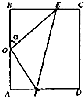
ij����ũׯ��һ�鳤��������ABCD��AB=100�ף�BC=50$\sqrt{3}$�ף�Ϊ�˱����ο�����ɢ������ũׯ�����������ڽ�3����ͼ��ʾ�Ĺ۹�����OE��EF��OF�����ǵ�����滮��Ҫ��O��AB���е㣬��E�ڱ�BC�ϣ���F�ڱ�AD�ϣ��������㣩���ҡ�EOF=90�㣮��$\sqrt{2}$��1.4��$\sqrt{3}$��1.7������ ��1��Ҫ����OEF���ܳ�l��ʾ�ɦ��ĺ�����ϵʽ����ѡ�OEF�����߷ֱ��ú��Ц��Ĺ�ϵʽ����ʾ����OE��OF���ֱ������Rt��OBE��Rt��OAF����⣬���ù��ɶ�������EF���Ӷ�����
��2����·�ܷ�����ͣ�ֻҪ���OEF���ܳ�l����Сֵ���ɣ��ɣ�1����l=$\frac{50��sin��+cos��+1��}{sin��cos��}$������[$\frac{��}{6}��\frac{��}{3}$]�����û�Ԫ����sin��+cos��=t����sin��cos��=$\frac{{t}^{2}-1}{2}$���Ӷ�ת��Ϊ�����ڱ������ϵ���Сֵ��
��� 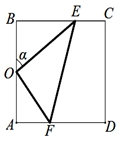 �⣺��1������Rt��BOE�У�OB=50����B=90�㣬��BOE=����
�⣺��1������Rt��BOE�У�OB=50����B=90�㣬��BOE=����
��OE=$\frac{50}{cos��}$
��Rt��AOF�У�OA=50����A=90�㣬��AFO=����
��OF=$\frac{50}{sin��}$��
�֡�EOF=90�㣬
��EF=$\sqrt{{OE}^{2}+{OF}^{2}}$=$\frac{50}{sin��cos��}$��
��l=OE+OF+EF=$\frac{50��sin��+cos��+1��}{sin��cos��}$��
����F�ڵ�Dʱ����ʱ�Ǧ���С����ʱ��=$\frac{��}{6}$��
����E��C��ʱ����ʱ�Ǧ������ô�ʱ��=$\frac{��}{3}$��
�ʴ˺����Ķ�����Ϊ[$\frac{��}{6}��\frac{��}{3}$]��
��2��������֪��Ҫ����·�ܷ�����ͣ�ֻҪ���OEF���ܳ�l����Сֵ���ɣ�
�ɣ�1���ã�l=$\frac{50��sin��+cos��+1��}{sin��cos��}$������[$\frac{��}{6}��\frac{��}{3}$]��
��sin��+cos��=t����sin��cos��=$\frac{{t}^{2}-1}{2}$��
��l=$\frac{50��sin��+cos��+1��}{sin��cos��}$=$\frac{100}{t-1}$
��t=sin��+cos��=$\sqrt{2}$sin����+$\frac{��}{4}$����
��$\frac{5��}{12}$�ܦ�+$\frac{��}{4}$��$\frac{7��}{12}$����$\frac{\sqrt{3}+1}{2}$��t��$\sqrt{2}$��
��$\frac{\sqrt{3}-1}{2}$��t-1��$\sqrt{2}$-1��
�Ӷ�����=$\frac{��}{4}$����BE=25ʱ��lmin=50��$\sqrt{2}$+1����
���Ե�BE=AF=25��ʱ����·�ܷ�����ͣ�����ܷ���Ϊ200000��$\sqrt{2}$+1��Ԫ��
���� ������Ҫ�����˽��������Ǻ�������������ʵ�������е�Ӧ�ã�������������ѧ֪ʶ���ʵ������������������������������


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{1}{4}$ | C�� | $1-\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{375��}{4}$ | B�� | 100�� | C�� | $\frac{250\sqrt{2}��}{3}$ | D�� | $\frac{500��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 0 | 1 | 2 | 3 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | -3 | C�� | $\frac{2}{3}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2ֻȫ�ǻ��ĸ��� | B�� | 2��ȫ�Ǻõĸ��� | ||
| C�� | ǡ��1ֻ�ǻ��ĸ��� | D�� | ����1ֻ�ǻ��ĸ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com