
 如图所示,A,B,C是一条公路上的三点,BC=2AB=2km,从这三点分别观测一塔P,从A测得塔在北偏东60°,从B测得塔在正东,从C测得塔在南偏东60°,求该塔到这条公路的距离.
如图所示,A,B,C是一条公路上的三点,BC=2AB=2km,从这三点分别观测一塔P,从A测得塔在北偏东60°,从B测得塔在正东,从C测得塔在南偏东60°,求该塔到这条公路的距离. 分析 过C,B,P分别作CMl,BNl,PQl,垂足分别为M,N,Q,设BN=x,可求PA,PC,由余弦定理可得AC2=PA2+PC2-2PA•PC•cos60°,解得x,过P作PD⊥AC,垂足为D,可求sin∠BAN=x,cos∠BAN=$\sqrt{1-{x}^{2}}$,sin∠CAP=$\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x,由PD=APsin∠CAP即可求值得解.
解答 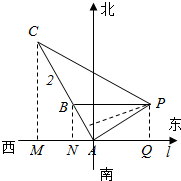 解:如图所示,过C,B,P分别作CMl,BNl,PQl,垂足分别为M,N,Q,设BN=x,即PQ=x,PA=2x,
解:如图所示,过C,B,P分别作CMl,BNl,PQl,垂足分别为M,N,Q,设BN=x,即PQ=x,PA=2x,
∵BC=2AB=2,
CM=3BN=3x,PC=2(MC-BN)=4x,
在△PAC中,由余弦定理可得:AC2=PA2+PC2-2PA•PC•cos60°,
即:9=4x2+16x2-2×2x×4x×$\frac{1}{2}$,
解得:x2=$\frac{3}{4}$,
过P作PD⊥AC,垂足为D,则线段PD的长为塔到直路的距离,
∵sin∠BAN=x,cos∠BAN=$\sqrt{1-{x}^{2}}$,
∴sin∠CAP=sin(150°-∠BAN)=$\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x,
∴PD=APsin∠CAP=2x×($\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x)=x$\sqrt{1-{x}^{2}}$+$\sqrt{3}$x2=$\sqrt{3}$.
点评 本题主要考查了余弦定理在解三角形中的应用,考查了同角三角函数关系式的应用,考查了数形结合思想和计算能力,属于基本知识的考查.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com