
【题目】如图,四棱锥P﹣ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.
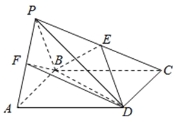
(Ⅰ)若点E是PC的中点,求证:PA∥平面BDE;
(Ⅱ)若点F在线段PA上,且FA=λPA,当三棱锥B﹣AFD的体积为![]() 时,求实数λ的值.
时,求实数λ的值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)连接AC,设AC∩BD=Q,又点E是PC的中点,则在△PAC中,中位线EQ∥PA,又EQ平面BDE,PA平面BDE.所以PA∥平面BDE;(Ⅱ)由平面PAB⊥平面ABCD,则PO⊥平面ABCD;作FM∥PO于AB上一点M,则FM⊥平面ABCD,进一步利用![]() 求得
求得![]() 最后利用平行线分线段成比例求出λ的值
最后利用平行线分线段成比例求出λ的值
试题解析:(Ⅰ)连接AC,设AC∩BD=Q,又点E是PC的中点,则在△PAC中,中位线EQ∥PA,
又EQ平面BDE,PA平面BDE.所以PA∥平面BDE
(Ⅱ)解:依据题意可得:PA=AB=PB=2,取AB中点O,
所以PO⊥AB,且![]() 又平面PAB⊥平面ABCD,则PO⊥平面ABCD;
又平面PAB⊥平面ABCD,则PO⊥平面ABCD;
作FM∥PO于AB上一点M,则FM⊥平面ABCD,因为四边形ABCD是矩形,
所以BC⊥平面PAB,则△PBC为直角三角形,
所以![]() ,则直角三角形△ABD的面积为
,则直角三角形△ABD的面积为![]() ,
,
![]()
由FM∥PO得: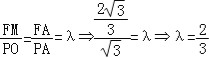


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y﹣1=0,l2:2x+ny+5=0,l3:mx+3y+1=0,若l1∥l2且l1⊥l3,则m+n的值为( )
A.﹣10B.﹣2C.2D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式: 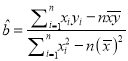 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() 三个数中任取的一个数,求
三个数中任取的一个数,求![]() 不为空集的概率;
不为空集的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 不为空集的概率.
不为空集的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com