
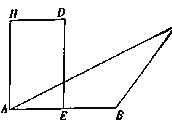
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,四边形
,四边形![]() 为矩形,固定边
为矩形,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,点
取得最小值时,点![]() 到直线
到直线![]() 的距离为__________.
的距离为__________.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间与极值;
的单调区间与极值;
(2)当![]() 时,令
时,令![]() ,若
,若![]() 在
在![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图像上所有点都在不等式组
的图像上所有点都在不等式组![]() 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax(a∈R).
(1)当a=3时,求函数f(x)在[![]() ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(2)当函数f(x)在(![]() ,2)单调时,求a的取值范围.
,2)单调时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5---10 | 6.5---8.5 |
某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是:未来一年内,位于一类风区的A项目获利![]() %的可能性为0.6,亏损
%的可能性为0.6,亏损![]() %的可能性为0.4;
%的可能性为0.4;
B项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2.
假设投资A项目的资金为![]() (
(![]() )万元,投资B项目资金为
)万元,投资B项目资金为![]() (
(![]() )万元,且公司要求对A项目的投资不得低于B项目.
)万元,且公司要求对A项目的投资不得低于B项目.
(Ⅰ)记投资A,B项目的利润分别为![]() 和
和![]() ,试写出随机变量
,试写出随机变量![]() 与
与![]() 的分布列和期望
的分布列和期望![]() ,
, ![]() ;
;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和![]() 的最大值,并据此给出公司分配投资金额建议.
的最大值,并据此给出公司分配投资金额建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线方程:
(1)求经过直线l1:x+3y﹣3=0,l2:x﹣y+1=0的交点,且平行于直线2x+y﹣3=0的直线l方程;
(2)求在两坐标轴上截距相等,且与点A(3,1)的距离为![]() 的直线l的方程.
的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,点M,N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( ) 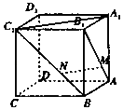
A.5
B.4
C.3
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com