
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:![]() 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图:
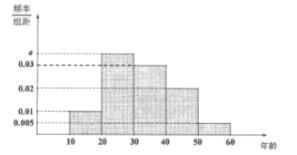
(1)求![]() 的值;
的值;
(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年北京市进行人口抽样调查,随机抽取了某区居民
年北京市进行人口抽样调查,随机抽取了某区居民![]() 人,记录他们的年龄,将数据分成
人,记录他们的年龄,将数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,…
,…![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从该区中随机抽取一人,估计其年龄不小于![]() 的概率;
的概率;
(Ⅱ)估计该区居民年龄的中位数(精确到![]() );
);
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,估计该区居民的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为x,求x≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知![]() ,函数
,函数![]() .
.
(I)当![]() 为何值时,
为何值时, ![]() 取得最大值?证明你的结论;
取得最大值?证明你的结论;
(II) 设![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围;
的取值范围;
(III)设![]() ,当
,当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com