
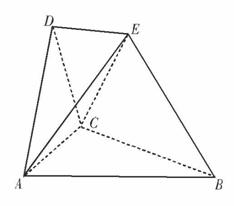
(理科)(13分)在如图所示的空间几何体中,平面![]() 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.
(1)求证:DE//平面ABC;(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积.
(理科)解:(1)由题意知, ![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,
取AC中点O,连接BO,DO,则![]()
![]() 平面ACD
平面ACD![]() 平面ABC
平面ABC
![]() 平面ABC,作EF
平面ABC,作EF![]() 平面ABC,
平面ABC,
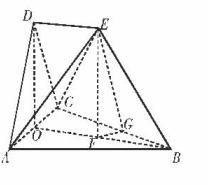 那么EF//DO,根据题意,点F落在BO上,
那么EF//DO,根据题意,点F落在BO上,
![]() ,易求得
,易求得![]()
所以四边形DEFO是平行四边形,DE//OF;
![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
![]() 平面ABC…………4分
平面ABC…………4分
(2)作FG![]() BC,垂足为G,连接FG;
BC,垂足为G,连接FG;
![]() 平面ABC,根据三垂线定理可知,EG
平面ABC,根据三垂线定理可知,EG![]() BC
BC
![]() 就是二面角E—BC—A的平面角
就是二面角E—BC—A的平面角
![]()
![]()
![]()
即二面角E—BC—A的余弦值为![]() …………8分
…………8分
(3)![]() 平面ACD
平面ACD![]() 平面ABC,OB
平面ABC,OB![]() AC
AC
![]() 平面ACD;又
平面ACD;又![]()
![]() 平面DAC,
平面DAC,![]() 三棱锥E—DAC的体积
三棱锥E—DAC的体积
![]()
又三棱锥E—ABC的体积![]()
![]() 多面体DE—ABC的体积为V=V1-V2=
多面体DE—ABC的体积为V=V1-V2=![]() …………13分
…………13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
 (理科)2013年将举办的第十二届中国•东海国际水晶节,主题为“水晶之都•福如东海”,于9月28日在国内唯一水晶博物馆正式开幕.为方便顾客,在休息区200m2的矩形区域内布置了如图所示的休闲区域(阴影部分),已知下方是两个相同的矩形.在休闲区域四周各留下1m宽的小路,若上面矩形部分与下方矩形部分高度之比为1:2.问如何设计休息区域,可使总休闲区域面积最大.
(理科)2013年将举办的第十二届中国•东海国际水晶节,主题为“水晶之都•福如东海”,于9月28日在国内唯一水晶博物馆正式开幕.为方便顾客,在休息区200m2的矩形区域内布置了如图所示的休闲区域(阴影部分),已知下方是两个相同的矩形.在休闲区域四周各留下1m宽的小路,若上面矩形部分与下方矩形部分高度之比为1:2.问如何设计休息区域,可使总休闲区域面积最大.查看答案和解析>>
科目:高中数学 来源:江苏省徐州市丰县修远双语学校2011-2012学年高二上学期第二次月考数学试题 题型:044
(理科做)
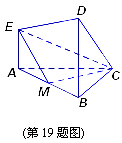
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.建立适当的空间直角坐标系,解决下列问题:
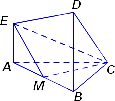
(1)求证:CM⊥EM;
(2)求CM与平面CDE所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二第二次月考数学试卷 题型:解答题
(本小题满分16分)(理科做)在如图所示的几何体中,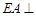 平面
平面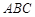 ,
,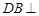 平面
平面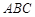 ,
,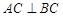 ,
,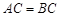
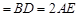 ,
, 是
是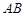 的中点.建立适当的空间直角坐标系,解决下列问题:
的中点.建立适当的空间直角坐标系,解决下列问题:
⑴求证: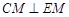 ;
;
⑵求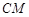 与平面
与平面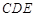 所成角的大小.
所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com