
【题目】某种商品每件进价9元,售价20元,每天可卖出69件.若售价降低,销售量可以增加,且售价降低![]() 元时,每天多卖出的件数与
元时,每天多卖出的件数与![]() 成正比.已知商品售价降低3元时,一天可多卖出36件.
成正比.已知商品售价降低3元时,一天可多卖出36件.
(Ⅰ)试将该商品一天的销售利润表示成![]() 的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
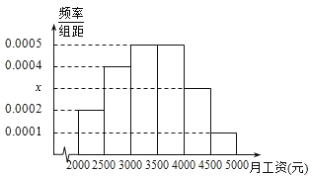
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
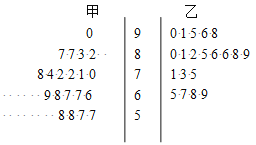
(1)学校规定:成绩不低于75分的为优秀.请画出下面的![]() 列联表.
列联表.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若双曲线![]() 的右焦点即为曲线
的右焦点即为曲线![]() 的右顶点,直线
的右顶点,直线![]() 为
为![]() 的一条渐近线.
的一条渐近线.
①.求双曲线C的方程;
②.过点![]() 的直线
的直线![]() ,交双曲线
,交双曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点(
点(![]() 点与
点与![]() 的顶点不重合),当
的顶点不重合),当![]() ,且
,且![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 的两条对角线
的两条对角线![]() 相交于
相交于![]() ,现用五种颜色(其中一种为红色)对图中四个三角形
,现用五种颜色(其中一种为红色)对图中四个三角形![]() 进行染色,且每个三角形用一种颜色图染.
进行染色,且每个三角形用一种颜色图染.
(1)若必须使用红色,求四个三角形![]() 中有且只有一组相邻三角形同色的染色方法的种数;
中有且只有一组相邻三角形同色的染色方法的种数;
(2)若不使用红色,求四个三角形![]() 中所有相邻三角形都不同色的染色方法的种数.
中所有相邻三角形都不同色的染色方法的种数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的1 000位上网购物者的年龄情况如图所示.
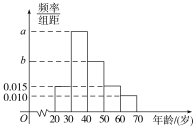
(1)已知[30,40),[40,50),[50,60)三个年龄段的上网购物者人数成等差数列,求a,b的值;
(2)该电子商务平台将年龄在[30,50)内的人群定义为高消费人群,其他年龄段的人群定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1 000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此3人获得代金券总和X(单位:元)的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com