
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用积分求出b,c,画出函数f(x)的图象,数形结合可得答案.
解答 解:∵b=$\frac{2}{π}$${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{2}{π}$•$\frac{1}{4}$•π•22=2,c=${∫}_{0}^{π}$sinxdx=-(cosπ-cos0)=2,
∴函数f(x)=$\left\{\begin{array}{l}{x}^{2}+2x-2,≤0\\ lgx,x>0\end{array}\right.$的图象如下图所示: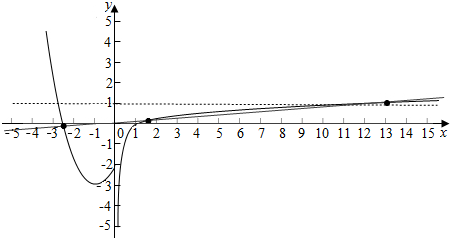
由图可得函数f(x)与函数y=$\frac{x}{4π}$的图象共有三个交点,
故函数g(x)=f(x)-$\frac{x}{4π}$有三个零点,
故选:C
点评 本题考查的知识点是函数零点及零点个数的判断,数形结合思想,积分运算,难度中档.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,$\frac{1}{2}$} | B. | {1,2} | C. | {0,1,2} | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
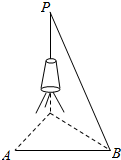 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
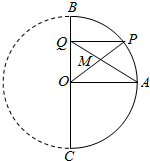 如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.
如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是某圆拱桥的示意图,这个圆拱桥的水面跨度AB=24m,拱高OP=8m.问:为使宽为10m的船能从桥下顺利通过,应如何限制船体及装载的货物在水面以上的高度?
如图是某圆拱桥的示意图,这个圆拱桥的水面跨度AB=24m,拱高OP=8m.问:为使宽为10m的船能从桥下顺利通过,应如何限制船体及装载的货物在水面以上的高度?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,4} | C. | {1} | D. | {2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com