
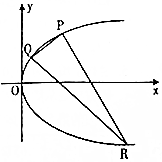
 已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.
已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.分析 (Ⅰ)直线y=2符合题意,当y≠2时,设l的方程m(y-2)=x-1,代入抛物线方程,由△=0,即可求得m的值,直线l的方程;
(Ⅱ)由$\overrightarrow{PQ}$=($\frac{{a}^{2}}{4}$-1,a-2),$\overrightarrow{PR}$=($\frac{{b}^{2}}{4}$-1,b-2),则$\overrightarrow{PQ}$•$\overrightarrow{PR}$=0,则ab+2a+2b+20=0,而过QR的直线的斜率为:$\frac{a-b}{\frac{{a}^{2}}{4}-\frac{{b}^{2}}{4}}$=$\frac{4}{a+b}$,整理得4x-20-(a+b)(y+2)=0.可得直线恒过定点(5,-2).
解答 解:(Ⅰ)由题意可知P(1,2),显然直线y=2符合题意;
当y≠2时,设l的方程m(y-2)=x-1,
$\left\{\begin{array}{l}{m(y-2)=x-1}\\{{y}^{2}=4x}\end{array}\right.$,整理得:y2-4my+8m-4=0,
令△=(4m)2-4(8m-4)=0,解得:m=1,
∴y=x+1,
∴直线l的方程y=2或y=x+1;
(Ⅱ)证明:设Q($\frac{{a}^{2}}{4}$,a),R($\frac{{b}^{2}}{4}$,b),而P(1,2),
∴$\overrightarrow{PQ}$=($\frac{{a}^{2}}{4}$-1,a-2),$\overrightarrow{PR}$=($\frac{{b}^{2}}{4}$-1,b-2),
由于PQ⊥PR,得向量$\overrightarrow{PQ}$•$\overrightarrow{PR}$=0,
即为($\frac{{a}^{2}}{4}$-1)($\frac{{b}^{2}}{4}$-1)+(a-2)(b-2)=0,
整理得ab+2a+2b+20=0.
而过QR的直线的斜率为:$\frac{a-b}{\frac{{a}^{2}}{4}-\frac{{b}^{2}}{4}}$=$\frac{4}{a+b}$.
∴过QR的直线方程为y-b=$\frac{4}{a+b}$(x-$\frac{{b}^{2}}{4}$),
整理得:4x+ab-(a+b)y=0,
即4x-(a+b)y-2a-2b-20=0.
化为4x-20-(a+b)(y+2)=0.可得直线恒过定点(5,-2).
∴直线QR必过定点(5,-2).
点评 本题考查了抛物线的简单几何性质,考查了直线系方程的运用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
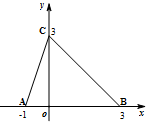
| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 因为f(0)?f(2)>0,所以f(x)在(0,2)内没有零点 | |
| B. | 因为1是f(x)的一个零点,所以f(0)?f(2)<0 | |
| C. | 由于f(x)在区间(-∞,0)上单调递减,所以f(x)在(-∞,0)内有唯一的一个零点 | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | $-\frac{12}{13}$ | C. | $\frac{12}{13}$ | D. | $-\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
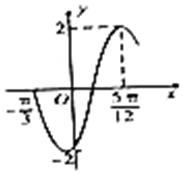 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com