
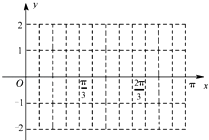
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图.
)的部分图象如图. 
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间.
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间.
【答案】
(1)解:根据f(x)的图象可得 ![]() T=
T= ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]() ,∴ω=1.
,∴ω=1.
根据五点法作图可得 1× ![]() +φ=
+φ= ![]() ,求得 φ=
,求得 φ= ![]() .
.
再把(0,1)代入函数的解析式可得 Asin ![]() =1,求得A=2,故f(x)=2sin(x+
=1,求得A=2,故f(x)=2sin(x+ ![]() ).
).
(2)解:将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,
倍,
可得y=2sin(2x+ ![]() )的图象;
)的图象;
再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)=2sin[2(x﹣
个单位,得到函数y=g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]=2sin(2x﹣
]=2sin(2x﹣ ![]() )的图象.
)的图象.
令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得 kπ﹣
,求得 kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
故g(x)的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈z.
],k∈z.
【解析】(1)由周期求出ω,由五点法作图求出φ的值,再把(0,1)代入函数的解析式求得A的值,可得函数f(x)的解析式.(2)由题意根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得x的范围,可得g(x)的增区间.
,求得x的范围,可得g(x)的增区间.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,85],得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足不等式|x﹣A|<B(A∈R,B>0)的实数x的集合叫做A的B 邻域.若a+b﹣t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是 ![]() .
. 
(1)求φ;
(2)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)求函数f(x)≥1(x∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且其6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com