
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|2x﹣3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
【答案】
(1)
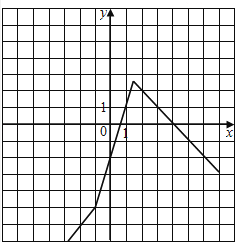
解:f(x)= 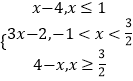 , 由分段函数的图象画法,可得f(x)的图象,如右:
, 由分段函数的图象画法,可得f(x)的图象,如右:
(2)
解:由|f(x)|>1,可得
当x≤﹣1时,|x﹣4|>1,解得x>5或x<3,即有x≤﹣1;
当﹣1<x< ![]() 时,|3x﹣2|>1,解得x>1或x<
时,|3x﹣2|>1,解得x>1或x< ![]() ,
,
即有﹣1<x< ![]() 或1<x<
或1<x< ![]() ;
;
当x≥ ![]() 时,|4﹣x|>1,解得x>5或x<3,即有x>5或
时,|4﹣x|>1,解得x>5或x<3,即有x>5或 ![]() ≤x<3.
≤x<3.
综上可得,x< ![]() 或1<x<3或x>5.
或1<x<3或x>5.
则|f(x)|>1的解集为(﹣∞, ![]() )∪(1,3)∪(5,+∞)
)∪(1,3)∪(5,+∞)
【解析】(Ⅰ)运用分段函数的形式写出f(x)的解析式,由分段函数的画法,即可得到所求图象;(2)分别讨论当x≤﹣1时,当﹣1<x< ![]() 时,当x≥
时,当x≥ ![]() 时,解绝对值不等式,取交集,最后求并集即可得到所求解集.;本题考查绝对值函数的图象和不等式的解法,注意运用分段函数的图象的画法和分类讨论思想方法,考查运算能力,属于基础题.
时,解绝对值不等式,取交集,最后求并集即可得到所求解集.;本题考查绝对值函数的图象和不等式的解法,注意运用分段函数的图象的画法和分类讨论思想方法,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆C: ![]() +y2=1(a>1)
+y2=1(a>1)
(1)求直线y=kx+1被椭圆截得到的弦长(用a,k表示)
(2)若任意以点A(0,1)为圆心的圆与椭圆至多有三个公共点,求椭圆的离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x-2sin2x-a.
①若f(x)=0在x∈R上有解,则a的取值范围是______;
②若x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,则sin(x1+x2)=______
]内的两个零点,则sin(x1+x2)=______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(cosθ,sinθ),
=(cosθ,sinθ),![]() =(cosβ,sinβ).
=(cosβ,sinβ).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 记f(θ)=
记f(θ)=![]() ,θ∈[0,
,θ∈[0,![]() ].当1≤λ≤2时,求f(θ)的最小值.
].当1≤λ≤2时,求f(θ)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(0,-2),椭圆E: ![]() 的离心率为
的离心率为![]() ,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A. 由“a(b+c)=ab+ac”类比推出“cos(α+β)=cosα+cosβ”
B. 由“若3a<3b,则a<b”类比推出“若ac<bc,则a<b”
C. 由“平面中垂直于同一直线的两直线平行”类比推出“空间中垂直于同一平面的两平面平行”
D. 由“等差数列{an}中,若a10=0,则a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)”类比推出“在等比数列{bn}中,若b9=1,则有b1b2…bn=b1b2…b17-n(n<17,n∈N*)”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com