
【题目】函数![]() .
.
(I)函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求a的值;
垂直,求a的值;
(II)讨论函数![]() 的单调性;
的单调性;
(III)不等式![]() 在区间
在区间![]() 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
【答案】(I)![]() (II)当
(II)当![]() 时,函数f(x)在区间
时,函数f(x)在区间![]() 上是单调递增;
上是单调递增;
当![]() 时,函数f(x)在区间
时,函数f(x)在区间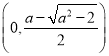 上单调递增;在区间
上单调递增;在区间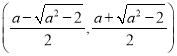 上单调递减;在区间
上单调递减;在区间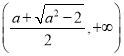 上单调递增(III)
上单调递增(III)![]() .
.
【解析】试题分析:(I)求导,利用导数的几何意义与两直线垂直的判定进行求解;(II)求导,讨论二次方程的根的个数、根的大小关系,进而判定其单调性;(III)分离常数,转化为求函数的求值问题.
试题解析:(I)函数![]() 定义域为
定义域为![]()
由题意![]() ,解得
,解得![]() .
.
(II)![]()
(i)当![]() 时,,函数f(x) 在
时,,函数f(x) 在![]() 上单调递增;
上单调递增;
(ii)当![]() 时,函数f(x)在区间
时,函数f(x)在区间 上单调递增;在区间
上单调递增;在区间 上单调递减;在区间
上单调递减;在区间 上单调递增
上单调递增
(iii)当![]() 时,,函数f(x) 在
时,,函数f(x) 在![]() 上单调递增;
上单调递增;
综上所述:当![]() 时,函数f(x)在区间
时,函数f(x)在区间![]() 上是单调递增;
上是单调递增;
当![]() 时,函数f(x)在区间
时,函数f(x)在区间 上单调递增;在区间
上单调递增;在区间 上单调递减;在区间
上单调递减;在区间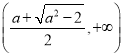 上单调递增
上单调递增
(III)等价于![]()
令![]()
在区间(0,1)上,函数g(x)为减函数;
在区间![]() 上,函数g(x)为增函数;
上,函数g(x)为增函数;
所以实数![]() 的范围是
的范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x ![]() (m∈Z)为偶函数,且在(0,+∞)上为增函数.
(m∈Z)为偶函数,且在(0,+∞)上为增函数.
(1)求m的值,并确定f(x)的解析式;
(2)若函数g(x)=loga(f(x)﹣ax+2)在区间(1,+∞)上恒为正值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列各式的值,写出必要的计算过程.
(1)0.064 ![]() ﹣(﹣
﹣(﹣ ![]() )0+16
)0+16 ![]() +0.25
+0.25 ![]()
(2)(log43+log83)(log32+log92)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为an的一组正三角形AnBn﹣1Bn的底边Bn﹣1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为2的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:y2=2px与椭圆C2: ![]() 在第一象限的交点为B,O为坐标原点,A为椭圆的右顶点,△OAB的面积为
在第一象限的交点为B,O为坐标原点,A为椭圆的右顶点,△OAB的面积为 ![]() .
. 
(1)求抛物线C1的方程;
(2)过A点作直线L交C1于C、D两点,求线段CD长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
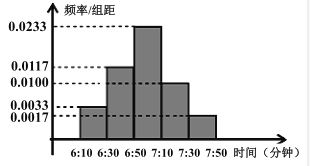
【题目】小明家订了一份报纸,暑假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数![]() 和中位数
和中位数![]() (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间![]() 在上午
在上午![]() 至
至![]() 之间,而送报人每天在
之间,而送报人每天在![]() 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件![]() )的概率.
)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C 的参数方程为 (
(![]() 为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)设![]() ,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com