
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
【答案】(1)m(t)=![]() (2)a≤2
(2)a≤2![]() -2.(3)a≤2
-2.(3)a≤2![]() -2.
-2.
【解析】
(1)是研究在动区间上的最值问题,这类问题的研究方法就是通过讨论函数的极值点与所研究的区间的大小关系来进行求解.
(2)注意到函数h(x)的图像上任意不同两点A,B连线的斜率总大于1,等价于h(x1)-h(x2)<x1-x2(x1<x2)恒成立,从而构造函数F(x)=h(x)-x在(0,+∞)上单调递增,进而等价于F′(x)≥0在(0,+∞)上恒成立来加以研究.
(3)用处理恒成立问题来处理有解问题,先分离变量转化为求对应函数的最值,得到a≤![]() ,再利用导数求函数M(x)=
,再利用导数求函数M(x)=![]() 的最大值,这要用到二次求导,才可确定函数单调性,进而确定函数最值.
的最大值,这要用到二次求导,才可确定函数单调性,进而确定函数最值.
(1) f′(x)=1-![]() ,x>0,
,x>0,
令f′(x)=0,则x=1.
当t≥1时,f(x)在[t,t+1]上单调递增,f(x)的最小值为f(t)=t-lnt;
当0<t<1时,f(x)在区间(t,1)上为减函数,在区间(1,t+1)上为增函数,f(x)的最小值为f(1)=1.
综上,m(t)=![]()
(2)h(x)=x2-(a+1)x+lnx,
不妨取0<x1<x2,则x1-x2<0,
则由![]() ,可得h(x1)-h(x2)<x1-x2,
,可得h(x1)-h(x2)<x1-x2,
变形得h(x1)-x1<h(x2)-x2恒成立.
令F(x)=h(x)-x=x2-(a+2)x+lnx,x>0,
则F(x)=x2-(a+2)x+lnx在(0,+∞)上单调递增,
故F′(x)=2x-(a+2)+![]() ≥0在(0,+∞)上恒成立,
≥0在(0,+∞)上恒成立,
所以2x+![]() ≥a+2在(0,+∞)上恒成立.
≥a+2在(0,+∞)上恒成立.
因为2x+![]() ≥2
≥2![]() ,当且仅当x=
,当且仅当x=![]() 时取“=”,
时取“=”,
所以a≤2![]() -2.
-2.
(3)因为f(x)≥![]() ,所以a(x+1)≤2x2-xlnx.
,所以a(x+1)≤2x2-xlnx.
因为x∈(0,1],则x+1∈(1,2],所以x∈(0,1],使得a≤![]() 成立.
成立.
令M(x)=![]() ,则M′(x)=
,则M′(x)=![]() .
.
令y=2x2+3x-lnx-1,则由y′=![]() =0 可得x=
=0 可得x=![]() 或x=-1(舍).
或x=-1(舍).
当x∈![]() 时,y′<0,则函数y=2x2+3x-lnx-1在
时,y′<0,则函数y=2x2+3x-lnx-1在![]() 上单调递减;
上单调递减;
当x∈![]() 时,y′>0,则函数y=2x2+3x-lnx-1在
时,y′>0,则函数y=2x2+3x-lnx-1在![]() 上单调递增.
上单调递增.
所以y≥ln4-![]() >0,
>0,
所以M′(x)>0在x∈(0,1]时恒成立,
所以M(x)在(0,1]上单调递增.
所以只需a≤M(1),即a≤1.
所以实数a的最大值为1.


科目:高中数学 来源: 题型:
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下表:
未发病 | 发病 | 合计 | |
未注射疫苗 | 40 |
|
|
注射疫苗 | 60 |
|
|
合计 | 100 | 100 | 200 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
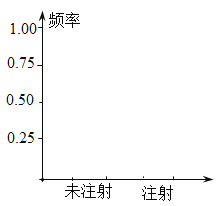
(2)在图中绘制发病率的条形统计图,并判断疫苗是否有效?
(3)在出错概率不超过![]() 的条件下能否认为疫苗有效?
的条件下能否认为疫苗有效?
附: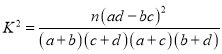 .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的平面展开图如图所示,其中四边形 ABCD 为正方形, E F 分别为PB PC 的中点,在此几何体中,下面结论中一定正确的是( )
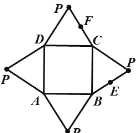
A.直线 AE 与直线 DF 平行B.直线 AE 与直线 DF 异面
C.直线 BF 和平面 PAD 相交D.直线 DF 平面 PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
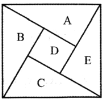
【题目】如图为我国数学家赵爽(约3世纪初)在为《周牌算经》作注时验证勾股定理的示意图,现在提供6种不同的颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() ,
,![]() 区域涂同色的概率为( )
区域涂同色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)求过点![]() 和函数
和函数![]() 的图像相切的直线方程;
的图像相切的直线方程;
(2)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在唯一的整数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面ABCD是边长为3的正方形,平面ADEF⊥平面ABCD,AF∥DE,AD⊥DE,AF=![]() ,DE=
,DE=![]() .
.
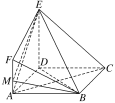
(1)求直线CA与平面BEF所成角的正弦值;
(2)在线段AF上是否存在点M,使得二面角MBED的大小为60°?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com