
【题目】已知直线![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对任意![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 单减,在
单减,在![]() 单增.(2)
单增.(2)![]()
【解析】
(1)求出f(x)的导数,得到f′(x),结合![]() 可解得
可解得![]() 与
与![]() 的范围,即可求出函数的单调区间.
的范围,即可求出函数的单调区间.
(2)通过讨论a的范围,得到导函数的正负,进而研究函数f(x)的单调性,求得不同情况下的函数f(x)的最小值,解出满足![]() 的a的范围即可.
的a的范围即可.
(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
,
而![]() ,且
,且![]() 在
在![]() 单调递增,所以当
单调递增,所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单减,在
单减,在![]() 单增.
单增.
(2)因为![]() ,
,![]() ,而当
,而当![]() 时,
时,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,
故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,符合题意,所以
,符合题意,所以![]() 符合题意.
符合题意.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,取
,取![]() ,则
,则![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
进而在![]() 单减,在
单减,在![]() 单增.
单增.
当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上单减,
上单减,
所以![]() .因而与题目要求在
.因而与题目要求在![]() ,
,![]() 恒成立矛盾,此类情况不成立,舍去.
恒成立矛盾,此类情况不成立,舍去.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某电视厂家准备在五一举行促销活动,现在根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:

(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(其中![]() ;参考方程:回归直线
;参考方程:回归直线 ,
,![]() )
)
(2)若用模型![]() 拟合y与x的关系,可得回归方程
拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的
,经计算线性回归模型和该模型的![]() 分别约为0.75和0.88,请用
分别约为0.75和0.88,请用![]() 说明选择哪个回归模型更好;
说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y﹣x.根据(2)的结果回答:当广告费x=20时,销售量及利润的预报值是多少?(精确到0.01)参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,现在沿
,现在沿![]() 将
将![]() 折起使点
折起使点![]() 到点P处,得到三棱锥
到点P处,得到三棱锥![]() ,且平面
,且平面![]() 平面
平面![]() .
.


(1)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?请说明你的结论;
?请说明你的结论;
(2)求证:![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
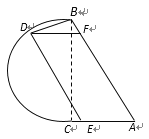
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
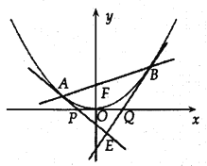
【题目】过抛物线![]() :
:![]() 的焦点
的焦点![]() 做直线
做直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,
两点,![]() 的最小值为2.
的最小值为2.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() ,
,![]() 分别做抛物线
分别做抛物线![]() 的切线,两切线交于点
的切线,两切线交于点![]() ,且直线
,且直线![]() ,
,![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,记
,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com