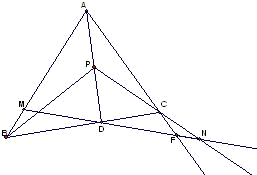
设D是△ABC的边BC上的一点,点P在线段AD上,过点D作一直线分别与线段AB、PB交于点M、E,与线段AC、PC的延长线交于点F、N.如果DE=DF,求证:DM=DN.
证明:对△AMD和直线BEP用梅涅劳斯定理得:
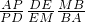
=1(1),
对△AFD和直线NCP用梅涅劳斯定理得:
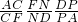
=1(2),
对△AMF和直线BDC用梅涅劳斯定理得:
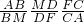
=1(3)
(1)(2)(3)式相乘得:
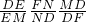
=1,
又DE=DF,
∴有
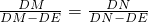
,
∴DM=DN.
分析:对于三个不同的三角形和对应的直线,应用梅涅劳斯定理,得到相应的三组线段之间比值的乘积是1,把三组比值的乘积相乘,约分整理,得到
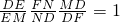
,根据DE=DF,约分得到最简形式,得到结果.
点评:本题考查梅涅劳斯定理,考查等量代换,考查整理比较麻烦的比例式时的方法,是一个基础题,题目的运算量比较大,是一个不常见到的题目.

 阅读快车系列答案
阅读快车系列答案