
 如图所示,正五边形ABCDE的每个顶点对应着一个整数,且这五个整数的和为正数.若其3个相邻顶点对应的整数依次为x、y、z,且y<0,则要进行如下的操作:把整数x、y、z分别换为x+y,-y,z+y,称其为一次“求正”操作.只要五个整数中有负整数,“求正”操作就要继续进行.
如图所示,正五边形ABCDE的每个顶点对应着一个整数,且这五个整数的和为正数.若其3个相邻顶点对应的整数依次为x、y、z,且y<0,则要进行如下的操作:把整数x、y、z分别换为x+y,-y,z+y,称其为一次“求正”操作.只要五个整数中有负整数,“求正”操作就要继续进行.
|


科目:高中数学 来源: 题型:
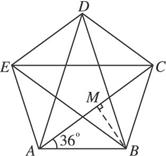
A.5 B.10 C.15 D.20
查看答案和解析>>
科目:高中数学 来源:2013年中国人民大学附中高三5月模拟数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com