
【题目】正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
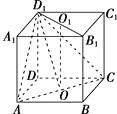
【解析】解法一:如图,设正方体的棱长为 ![]() ,上,下底面的中心分别为
,上,下底面的中心分别为 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() 与平面ACD1所成的角就是BB1与平面ACD1所成的角,即∠O1OD1 , cos∠O1OD1=
与平面ACD1所成的角就是BB1与平面ACD1所成的角,即∠O1OD1 , cos∠O1OD1= ![]() .
.
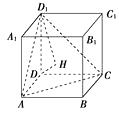
解法二:画出图形,如图,BB1与平面ACD1所成的角等于DD1与平面ACD1所成的角,在三棱锥D-ACD1中,由三条侧棱两两垂直且相等得点D在底面ACD1内的射影为等边三角形ACD1的重心,即中心H,连接D1H,DH,则∠DD1H为DD1与平面ACD1所成的角,设正方体的棱长为a,则cos∠DD1H= ![]() .
.
故答案为:D.
由正方体的结构特征,找到BB1在平面平面 AC D 1 内的射影为OD1,于是 ∠O1OD1就是所求的角,在对应三角形中求解。


科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,已知AD=2AB=2a,BD= ![]() ,AC∩BD=E,将其沿对角线BD折成直二面角.
,AC∩BD=E,将其沿对角线BD折成直二面角.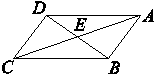
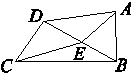
求证:
(1)AB⊥平面BCD;
(2)平面ACD⊥平面ABD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+bx+c(a,b,c∈R),若函数y=f(x)ex在x=﹣1处取得极值,则下列图象不可能为y=f(x)的图象是( )
A.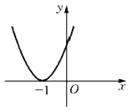
B.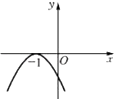
C.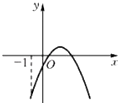
D.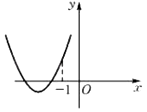
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,市电视台举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确将给该选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率均为 ![]() ;现记“该选手在回答完n个问题后的总得分为Sn”.
;现记“该选手在回答完n个问题后的总得分为Sn”.
(1)求S6=20且Si≥0(i=1,2,3)的概率;
(2)记X=|S5|,求X的分布列,并计算数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ ![]() (a∈R)是定义域为R的奇函数,其中e是自然对数的底数.
(a∈R)是定义域为R的奇函数,其中e是自然对数的底数.
(1)求实数a的值;
(2)若存在x∈(0,+∞),使不等式f(x2+x)+f(2﹣tx)<0成立,求实数t的取值范围;
(3)若函数y=e2x+ ![]() ﹣2mf(x)在(m,+∞)上不存在最值,求实数m的取值范围.
﹣2mf(x)在(m,+∞)上不存在最值,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com