
分析 (I)分别利用等差数列的求和公式及等比数列的通项公式表示已知条件,然后解方程可求等比数列的公比q,等差数列的公差d,即可求解;
(II)根据(1)中数列{an}的通项公式,运用等差数列的求和公式可得cn=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,利用裂项相消求和可得Tn.再由数列的单调性和不等式的性质,即可得证.
解答 解:(I)设等差数列{an}的公差为d,
∵等差数列{an}前n项和为Sn,数列{bn}为等比数列,且b2+S2=12,q=$\frac{{S}_{2}}{{b}_{2}}$,
∴$\left\{\begin{array}{l}{q+{a}_{1}+{a}_{2}=12}\\{q=\frac{{a}_{1}+{a}_{2}}{q}}\end{array}\right.$,即$\left\{\begin{array}{l}{q+6+d=12}\\{{q}^{2}=6+d}\end{array}\right.$,
解得d=q=3,
∴an=3+(n-1)•3=3n,bn=1•3n-1=3n-1;
(Ⅱ)证明:cn=$\frac{3}{2{S}_{n}}$=$\frac{3}{2•\frac{1}{2}n(3+3n)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
前n项和Tn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$,
数列{1-$\frac{1}{n+1}$}递增,即有n=1时取得最小值$\frac{1}{2}$,
则有$\frac{1}{2}$≤Tn<1.
点评 本题考查等差数列与等比数列的通项公式和前n项和公式,考查裂项相消求和的方法,考查方程思想与运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.
如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
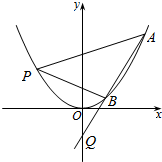 已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.
已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com