
”¾ĢāÄæ”æ¶ØŅå£ŗf1£Øx£©=f£Øx£©£¬µ±n”Ż2ĒŅx”ŹN*Ź±£¬fn£Øx£©=f£Øfn©1£Øx£©£©£¬¶ŌÓŚŗÆŹżf£Øx£©¶ØŅåÓņÄŚµÄx0 £¬ ČōÕżŌŚÕżÕūŹżnŹĒŹ¹µĆfn£Øx0£©=x0³ÉĮ¢µÄ×īŠ”ÕżÕūŹż£¬Ōņ³ĘnŹĒµćx0µÄ×īŠ”ÕżÖÜĘŚ£¬x0³ĘĪŖf£Øx£©µÄn”«ÖÜĘŚµć£¬ŅŃÖŖ¶ØŅåŌŚ[0£¬1]ÉĻµÄŗÆŹżf£Øx£©µÄĶ¼ĻóČēĶ¼£¬¶ŌÓŚŗÆŹżf£Øx£©£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£ØŠ“³öĖłÓŠÕżČ·ĆüĢāµÄ±ąŗÅ£©
¢Ł1ŹĒf£Øx£©µÄŅ»øö3”«ÖÜĘŚµć£»
¢Ś3ŹĒµć ![]() µÄ×īŠ”ÕżÖÜĘŚ£»
µÄ×īŠ”ÕżÖÜĘŚ£»
¢Ū¶ŌÓŚČĪŅāÕżÕūŹżn£¬¶¼ÓŠfn£Ø ![]() £©=
£©= ![]() £»
£»
¢ÜČōx0”Ź£Ø ![]() £¬1]£¬Ōņx0ŹĒf£Øx£©µÄŅ»øö2”«ÖÜĘŚµć£®
£¬1]£¬Ōņx0ŹĒf£Øx£©µÄŅ»øö2”«ÖÜĘŚµć£®
”¾“š°ø”æ¢Ł¢Ś¢Ū
”¾½āĪö”æ½ā£ŗf1£Ø1£©=f£Ø1£©=0£¬f2£Ø1£©=f£Øf1£Ø1£©£©=f£Ø0£©= ![]() £¬f3£Ø1£©=f£Øf2£Ø1£©£©=f£Ø
£¬f3£Ø1£©=f£Øf2£Ø1£©£©=f£Ø ![]() £©=1£¬¹Ź¢Ł1ŹĒf£Øx£©µÄŅ»øö3”«ÖÜĘŚµć£¬ÕżČ·£»
£©=1£¬¹Ź¢Ł1ŹĒf£Øx£©µÄŅ»øö3”«ÖÜĘŚµć£¬ÕżČ·£»
f1£Ø ![]() £©=f£Ø
£©=f£Ø ![]() £©=1£¬f2£Ø
£©=1£¬f2£Ø ![]() £©=f£Øf1£Ø
£©=f£Øf1£Ø ![]() £©£©=f£Ø1£©=0£¬f3£Ø
£©£©=f£Ø1£©=0£¬f3£Ø ![]() £©=f£Øf2£Ø
£©=f£Øf2£Ø ![]() £©£©=f£Ø0£©=
£©£©=f£Ø0£©= ![]() £¬
£¬
¹Ź¢Ś3ŹĒµć ![]() µÄ×īŠ”ÕżÖÜĘŚ£¬ÕżČ·£»
µÄ×īŠ”ÕżÖÜĘŚ£¬ÕżČ·£»
ÓÉŅŃÖŖÖŠµÄĶ¼ĻóæÉµĆ£ŗf£Ø ![]() £©=
£©= ![]() £¬
£¬
¹Źf1£Ø ![]() £©=f£Ø
£©=f£Ø ![]() £©=
£©= ![]() £¬f2£Ø
£¬f2£Ø ![]() £©=f£Øf1£Ø
£©=f£Øf1£Ø ![]() £©£©=f£Ø
£©£©=f£Ø ![]() £©=
£©= ![]() £¬f3£Ø
£¬f3£Ø ![]() £©=f£Øf2£Ø
£©=f£Øf2£Ø ![]() £©£©=f£Ø
£©£©=f£Ø ![]() £©=
£©= ![]() £¬
£¬
¹Ź¢Ū¶ŌÓŚČĪŅāÕżÕūŹżn£¬¶¼ÓŠfn£Ø ![]() £©=
£©= ![]() £¬ÕżČ·£»
£¬ÕżČ·£»
¢ÜČōx0=1£¬Ōņx0”Ź£Ø ![]() £¬1]£¬µ«x0ŹĒf£Øx£©µÄŅ»øö3”«ÖÜĘŚµć£¬¹Ź“ķĪó£®
£¬1]£¬µ«x0ŹĒf£Øx£©µÄŅ»øö3”«ÖÜĘŚµć£¬¹Ź“ķĪó£®
ĖłŅŌ“š°øŹĒ£ŗ¢Ł¢Ś¢Ū
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖĆüĢāµÄÕę¼ŁÅŠ¶ĻÓėÓ¦ÓƵÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕĮ½øöĆüĢā»„ĪŖÄę·ńĆüĢā£¬ĖüĆĒÓŠĻąĶ¬µÄÕę¼ŁŠŌ£»Į½øöĆüĢāĪŖ»„ÄęĆüĢā»ņ»„·ńĆüĢā£¬ĖüĆĒµÄÕę¼ŁŠŌƻӊ¹ŲĻµ²ÅÄÜÕżČ·½ā“š“ĖĢā£®


 »ĘøŌĢģĢģĮ·æŚĖćĢāæØĻµĮŠ“š°ø
»ĘøŌĢģĢģĮ·æŚĖćĢāæØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčDĪŖ²»µČŹ½×é 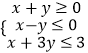 ±ķŹ¾µÄĘ½ĆęĒųÓņ£¬¶ŌÓŚĒųÓņDÄŚ³żŌµćĶāµÄČĪŅ»µćA£Øx£¬y£©£¬Ōņ2x+yµÄ×ī“óÖµŹĒ £¬
±ķŹ¾µÄĘ½ĆęĒųÓņ£¬¶ŌÓŚĒųÓņDÄŚ³żŌµćĶāµÄČĪŅ»µćA£Øx£¬y£©£¬Ōņ2x+yµÄ×ī“óÖµŹĒ £¬ ![]() µÄȔֵ·¶Ī§ŹĒ £®
µÄȔֵ·¶Ī§ŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚČżĄāÖłABC©A1B1C1ÖŠ£¬CA=CB£¬²ąĆęABB1A1ŹĒ±ß³¤ĪŖ2µÄÕż·½ŠĪ£¬µćE£¬F·Ö±šŌŚĻ߶ĪAAl £¬ A1B1ÉĻ£¬ĒŅAE= ![]() £¬A1F=
£¬A1F= ![]() £¬CE”ĶEF£¬MĪŖABÖŠµć £Ø¢ń£©Ö¤Ć÷£ŗEF”ĶĘ½ĆęCME£»
£¬CE”ĶEF£¬MĪŖABÖŠµć £Ø¢ń£©Ö¤Ć÷£ŗEF”ĶĘ½ĆęCME£»
£Ø¢ņ£©ČōCA”ĶCB£¬ĒóÖ±ĻßAC1ÓėĘ½ĆęCEFĖł³É½ĒµÄÕżĻŅÖµ£®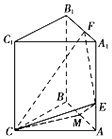
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖÄÖÖĖµ·ØÖŠ£¬
¢ŁĆüĢā”°“ęŌŚx”ŹR£¬x2©x£¾0”±µÄ·ń¶ØŹĒ”°¶ŌÓŚČĪŅāx”ŹR£¬x2©x£¼0”±£»
¢ŚĆüĢā”°pĒŅqĪŖÕę”±ŹĒ”°p»ņqĪŖÕę”±µÄ±ŲŅŖ²»³ä·ÖĢõ¼ž£»
¢ŪŅŃÖŖĆŻŗÆŹżf£Øx£©=x¦ĮµÄĶ¼Ļó¾¹żµć£Ø2£¬ ![]() £©£¬Ōņf£Ø4£©µÄÖµµČÓŚ
£©£¬Ōņf£Ø4£©µÄÖµµČÓŚ ![]() £»
£»
¢ÜŅŃÖŖĻņĮæ ![]() =£Ø3£¬©4£©£¬
=£Ø3£¬©4£©£¬ ![]() =£Ø2£¬1£©£¬ŌņĻņĮæ
=£Ø2£¬1£©£¬ŌņĻņĮæ ![]() ŌŚĻņĮæ
ŌŚĻņĮæ ![]() ·½ĻņÉĻµÄĶ¶Ó°ŹĒ
·½ĻņÉĻµÄĶ¶Ó°ŹĒ ![]() £®
£®
Ėµ·Ø“ķĪóµÄøöŹżŹĒ£Ø £©
A.1
B.2
C.3
D.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©=x©alnx£Øa”ŹR£©
£Ø1£©µ±a=2Ź±£¬ĒóĒśĻßy=f£Øx£©ŌŚµćA£Ø1£¬f£Ø1£©£©“¦µÄĒŠĻß·½³Ģ£»
£Ø2£©ĒóŗÆŹżf£Øx£©µÄ¼«Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤ŅÕĘ·³§ŅŖÉč¼ĘŅ»øöČēĶ¼¢ńĖłŹ¾µÄ¹¤ŅÕĘ·£¬ĻÖӊijÖÖŠĶŗŵij¤·½ŠĪ²ÄĮĻČēĶ¼¢ņĖłŹ¾£¬ĘäÖܳ¤ĪŖ4m£¬ÕāÖÖ²ÄĮĻŃŲĘä¶Ō½ĒĻßÕŪµžŗó¾Ķ³öĻÖĶ¼¢ńµÄĒéæö£®ČēĶ¼£¬ABCD£ØAB£¾AD£©ĪŖ³¤·½ŠĪµÄ²ÄĮĻ£¬ŃŲACÕŪµžŗóAB'½»DCÓŚµćP£¬Éč”÷ADPµÄĆ껿ĪŖ
S2 £¬ ÕŪµžŗóÖŲŗĻ²æ·Ö”÷ACPµÄĆ껿ĪŖS1 £®
£Ø¢ń£©ÉčAB=xm£¬ÓĆx±ķŹ¾Ķ¼ÖŠDPµÄ³¤¶Č£¬²¢Š“³öxµÄȔֵ·¶Ī§£»
£Ø¢ņ£©ĒóĆ껿S2×ī“óŹ±£¬Ó¦ŌõŃłÉč¼Ę²ÄĮĻµÄ³¤ŗĶæķ£æ
£Ø¢ó£©ĒóĆ껿£ØS1+2S2£©×ī“óŹ±£¬Ó¦ŌõŃłÉč¼Ę²ÄĮĻµÄ³¤ŗĶæķ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©=2sin¦Ųx£¬ĘäÖŠ³£Źż¦Ų£¾0£®
£Ø¢ń£©Įī¦Ų=1£¬ĒóŗÆŹż ![]() ŌŚ
ŌŚ ![]() ÉĻµÄ×ī“óÖµ£»
ÉĻµÄ×ī“óÖµ£»
£Ø¢ņ£©ČōŗÆŹż ![]() µÄÖÜĘŚĪŖ¦Š£¬ĒóŗÆŹżg£Øx£©µÄµ„µ÷µŻŌöĒų¼ä£¬²¢Ö±½ÓŠ“³ög£Øx£©ŌŚ
µÄÖÜĘŚĪŖ¦Š£¬ĒóŗÆŹżg£Øx£©µÄµ„µ÷µŻŌöĒų¼ä£¬²¢Ö±½ÓŠ“³ög£Øx£©ŌŚ ![]() µÄĮćµćøöŹż£®
µÄĮćµćøöŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚøß֊ѧĻ°¹ż³ĢÖŠ£¬Ķ¬Ń§ĆĒ¾³£ÕāŃłĖµ£ŗ”°ŹżŃ§ĪļĄķ²»·Ö¼Ņ£¬Čē¹ūĪļĄķ³É¼ØŗĆ£¬ÄĒƓѧĻ°ŹżŃ§¾ĶĆ»Ź²Ć“ĪŹĢā£®”±Ä³°ąÕė¶Ō”°øßÖŠÉśĪļĄķѧĻ°¶ŌŹżŃ§Ń§Ļ°µÄÓ°Ļģ”±½ųŠŠŃŠ¾æ£¬µĆµ½ĮĖĖÕ¶ķÉśµÄĪļĄķ³É¼ØÓėŹżŃ§³É¼Ø¾ßÓŠĻߊŌĻą¹Ų¹ŲĻµµÄ½įĀŪ£®ĻÖ“ÓøĆ°ąĖ껜³éČ”5ĆūѧɜŌŚŅ»“Īæ¼ŹŌÖŠµÄŹżŃ§ŗĶĪļĄķ³É¼Ø£¬Čē±ķ£ŗ
³É¼Ø ±ąŗÅ | 1 | 2 | 3 | 4 | 5 |
ĪļĄķ£Øx£© | 90 | 85 | 74 | 68 | 63 |
ŹżŃ§£Øy£© | 130 | 125 | 110 | 95 | 90 |
£Ø1£©ĒóŹżŃ§³É¼Øy¶ŌĪļĄķ³É¼ØxµÄĻߊŌ»Ų¹é·½³Ģ ![]() =
= ![]() x+
x+ ![]() £Ø
£Ø ![]() ¾«Č·µ½0.1£©£®ČōijĪ»Ń§ÉśµÄĪļĄķ³É¼ØĪŖ80·Ö£¬Ō¤²āĖūµÄŹżŃ§³É¼Ø£»
¾«Č·µ½0.1£©£®ČōijĪ»Ń§ÉśµÄĪļĄķ³É¼ØĪŖ80·Ö£¬Ō¤²āĖūµÄŹżŃ§³É¼Ø£»
£Ø2£©ŅŖ“Ó³éČ”µÄÕāĪåĪ»Ń§ÉśÖŠĖ껜є³ö2Ī»²Ī¼ÓŅ»ĻīÖŖŹ¶¾ŗČü£¬Ēóє֊µÄѧɜµÄŹżŃ§³É¼ØÖĮÉŁÓŠŅ»Ī»øßÓŚ120·ÖµÄøÅĀŹ£®£Ø²Īæ¼¹«Ź½£ŗ ![]() =
=  £¬
£¬ ![]() =
= ![]() ©
© ![]() £© £Ø²Īæ¼Źż¾Ż£ŗ902+852+742+682+632=29394£¬90”Į”Į125+74”Į110+68”Į95+63”Į90=42595£©
£© £Ø²Īæ¼Źż¾Ż£ŗ902+852+742+682+632=29394£¬90”Į”Į125+74”Į110+68”Į95+63”Į90=42595£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŗÆŹżf£Øx£©=x2©bx+cĀś×ćf£Ø1+x£©=f£Ø1©x£©ĒŅf£Ø0£©=3£¬Ōņf£Øbx£©ŗĶf£Øcx£©µÄ“󊔹ŲĻµŹĒ£Ø £©
A.f£Øbx£©”Üf£Øcx£©
B.f£Øbx£©”Żf£Øcx£©
C.f£Øbx£©£¾f£Øcx£©
D.“󊔹ŲĻµĖęxµÄ²»Ķ¬¶ų²»Ķ¬
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com