
设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=∠DBC=![]() ,求:
,求:
(1)直线AD与平面BCD所成角的大小;
(2)异面直线AD与BC所成的角;
(3)二面角A—BD—C的大小.
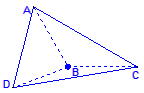
(1) 45° (2) AD与BC所成的角为90° (3) 二面角A—BD—C大小为π-arctan2.
(1)如图,在平面ABC内,过A作AH⊥BC,垂足为H,则AH⊥平面DBC,
∴∠ADH即为直线AD与平面BCD所成的角![]() 由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,
由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,
∴∠ADH=45°

(2)∵BC⊥DH,且DH为AD在平面BCD上的射影,
∴BC⊥AD,故AD与BC所成的角为90°。
(3)过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角![]() 设BC=a,则由题设知,AH=DH=
设BC=a,则由题设知,AH=DH=![]() ,在△HDB中,HR=
,在△HDB中,HR=![]() a,∴tanARH=
a,∴tanARH=![]() =2
=2
故二面角A—BD—C大小为π-arctan2.
另法(向量法): (略)



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:导学大课堂必修二数学苏教版 苏教版 题型:044
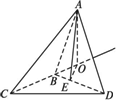
如下图,设△ABC和△DBC所在的两平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求二面角A-BD-C的平面角的补角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
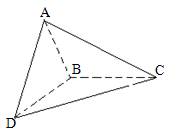
(08年唐山市一中调研一理) 设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=∠DBC=120°
(I)求证![]() ;
;
(II)求二面角A―BD―C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
设△ABC和△DBC所在两平面互相垂直,且AB=BC=BD=a,∠CBA=∠CBD=![]() ,则AD与平面BCD所成的角为( )
,则AD与平面BCD所成的角为( )
A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:高中数学 来源: 题型:
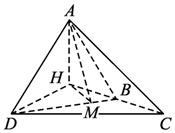
(1)A、D的连线和平面BCD所成的角;
(2)A、D的连线和直线BC所成的角;
(3)二面角A—BD—C的大小.(用反三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com