
【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
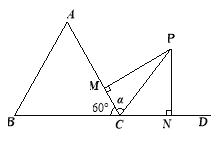
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


【答案】(1)![]() (2)α=
(2)α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() .
.
【解析】
试题分析:(1)解三角形,就是利用正余弦定理将边角统一,本题求角,应利用正弦定理将边化为角:sinAcosA=sinBcosB,再根据二倍角公式及诱导公式求角:sin2A=sin2B, A=B或A+B=![]() .因为C=
.因为C=![]() ,所以A=B,A=
,所以A=B,A=![]() .(2)求PM+PN的最大值,首先建立函数关系式,取自变量为角:PM+PN=2sinα+2sin (α+
.(2)求PM+PN的最大值,首先建立函数关系式,取自变量为角:PM+PN=2sinα+2sin (α+![]() )=3sinα+
)=3sinα+![]() cosα=2
cosα=2![]() sin(α+
sin(α+![]() ).再根据基本三角函数求其最值:因为α∈(0,
).再根据基本三角函数求其最值:因为α∈(0,![]() ),所以α+
),所以α+![]() ∈(
∈(![]() ,
,![]() ),从而有sin(α+
),从而有sin(α+![]() )∈(
)∈(![]() ,1],因此当α+
,1],因此当α+![]() =
=![]() ,即α=
,即α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() .
.
试题解析:(1)由acosA=bcosB及正弦定理可得sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
所以有A=B或A+B=![]() . 2分
. 2分
![]() ,得A+B=
,得A+B=![]() ,与A+B=
,与A+B=![]() 矛盾,所以A=B,
矛盾,所以A=B,
因此A=![]() . 4分
. 4分
(2)由题设,得
在Rt△PMC中,PM=PC·sin∠PCM=2sinα;
在Rt△PNC中,PN=PC·sin∠PCN= PC·sin(π-∠PCB)
=2sin[π-(α+![]() )]=2sin (α+
)]=2sin (α+![]() ),α∈(0,
),α∈(0,![]() ). 6分
). 6分
所以,PM+PN=2sinα+2sin (α+![]() )=3sinα+
)=3sinα+![]() cosα=2
cosα=2![]() sin(α+
sin(α+![]() ). 10分
). 10分
因为α∈(0,![]() ),所以α+
),所以α+![]() ∈(
∈(![]() ,
,![]() ),从而有sin(α+
),从而有sin(α+![]() )∈(
)∈(![]() ,1],
,1],
即2![]() sin(α+
sin(α+![]() )∈(
)∈(![]() ,2
,2![]() ].
].
于是,当α+![]() =
=![]() ,即α=
,即α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() . 14分
. 14分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+x,a∈R.
ax2+x,a∈R.
(1)若f(1)=0,求函数f(x)的最大值;
(2)令g(x)=f(x)﹣(ax﹣1),求函数g(x)的单调区间;
(3)若a=﹣2,正实数x1 , x2满足f(x1)+f(x2)+x1x2=0,证明x1+x2≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
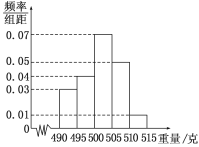
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三内角A,B,C所对的边分别是a,b,c,△ABC的面积S= ![]() 且sinA=
且sinA= ![]() .
.
(1)求sinB;
(2)若边c=5,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同, 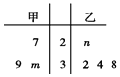
(1)求m,n的取值.
(2)比较甲、乙两组数据的稳定性,并说明理由.
注:方差公式s2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB= ![]() ,若点A的坐标为(
,若点A的坐标为( ![]() ,
, ![]() ),记∠COA=α.
),记∠COA=α. 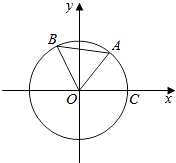
(1)求 ![]() 的值;
的值;
(2)求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com