
【题目】在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() .
.
(1)求以线段![]() 、
、![]() 为邻边的平行四边形两条对角线的长;
为邻边的平行四边形两条对角线的长;
(2)设![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() 、
、![]() ;(2)
;(2)![]() .
.
【解析】
(1)方法一:计算出向量![]() 、
、![]() ,利用平面向量的坐标运算可求出所求得的两条对角线
,利用平面向量的坐标运算可求出所求得的两条对角线![]() 和
和![]() 的长度;
的长度;
方法二:利用平行四边形的对角线互相平分可求出第四个顶点![]() 的坐标,然后利用两点间的距离公式可求得平行四边形两条对角线的长度;
的坐标,然后利用两点间的距离公式可求得平行四边形两条对角线的长度;
(2)求出向量![]() 的坐标,然后利用共线向量的坐标表示可得出关于实数
的坐标,然后利用共线向量的坐标表示可得出关于实数![]() 的方程,解出即可.
的方程,解出即可.
(1)(方法一)由题设知![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
故所求的两条对角线的长分别为![]() 、
、![]() ;
;
(方法二)设该平行四边形的第四个顶点为![]() ,两条对角线的交点为
,两条对角线的交点为![]() ,
,
则![]() 为
为![]() 、
、![]() 的中点,
的中点,![]() ,
,
又![]() 为
为![]() 的中点,则
的中点,则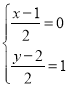 ,解得
,解得![]() ,则点
,则点![]() ,
,
由两点间的距离公式可得![]() ,
,
![]() ,
,
故所求的两条对角线的长分别为![]() 、
、![]() ;
;
(2)由题设知:![]() ,
,![]() .
.
由![]() ,得
,得![]() ,从而
,从而![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数 和
和![]() (
(![]() 且为常数),则下列结论正确的是( )
且为常数),则下列结论正确的是( )
A.当![]() 时,存在实数
时,存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不同的实数根
有四个不同的实数根
B.存在![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不同的实数根
有三个不同的实数根
C.当![]() 时,若函数
时,若函数![]() 恰有
恰有![]() 个不同的零点
个不同的零点![]() 、
、![]() 、
、![]() ,则
,则![]()
D.当![]() 时,且关于
时,且关于![]() 的方程
的方程![]() 有四个不同的实数根
有四个不同的实数根![]() 、
、![]() 、
、![]() 、
、![]()
![]() ,若
,若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区组织部为了了解全区科级干部“党风廉政知识”的学习情况,按照分层抽样的方法,从全区320名正科级干部和1280名副科级干部中抽取40名科级干部预测全区科级干部“党风廉政知识”的学习情况.现将这40名科级干部分为正科级干部组和副科级干部组,利用同一份试卷分别进行预测.经过预测后,两组各自将预测成绩统计分析如下表:
分组 | 人数 | 平均成绩 | 标准差 |
正科级干部组 |
| 80 | 6 |
副科级干部组 |
| 70 | 4 |
(1)求![]() ;
;
(2)求这40名科级干部预测成绩的平均分![]() 和标准差
和标准差![]() ;
;
(3)假设该区科级干部的“党风廉政知识”预测成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
.利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)完游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设![]() 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜,你认为此游戏是否公平,说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童玩具生产厂一车间计划每天生产遥控小车模型、遥控飞机模型、遥控火车模型这三种玩具共![]() 个,生产一个遥控小车模型需
个,生产一个遥控小车模型需![]() 分钟,生产一个遥控飞机模型需
分钟,生产一个遥控飞机模型需![]() 分钟,生产一个遥控火车模型需
分钟,生产一个遥控火车模型需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 分钟,若生产一个遥控小车模型可获利
分钟,若生产一个遥控小车模型可获利![]() 元,生产一个遥控飞机模型可获利
元,生产一个遥控飞机模型可获利![]() 元,生产一个遥控火车模型可获利
元,生产一个遥控火车模型可获利![]() 元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com