
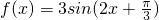 ,则以下不等式正确的是
,则以下不等式正确的是 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
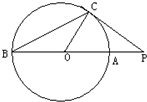 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 6 |
| a |
| m |
| 1 |
| n |
|
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川达州普通高中高三第一次诊断检测理科数学试卷(解析版) 题型:填空题
以下四个命题:
①函数 既无最小值也无最大值;
既无最小值也无最大值;
②在区间 上随机取一个数
上随机取一个数 ,使得
,使得 成立的概率为
成立的概率为 ;
;
③若不等式 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为16;
的最小值为16;
④已知函数 ,若方程
,若方程 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数 的取值范围是
的取值范围是 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三9月月考理科数学试卷 题型:填空题
若整数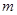 满足不等式
满足不等式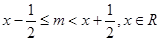 ,则称
,则称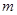 为
为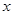 的“亲密整数”,记作
的“亲密整数”,记作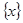 ,即
,即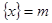 ,已知函数
,已知函数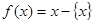 .给出以下四个命题:
.给出以下四个命题:
① 函数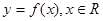 是周期函数且其最小正周期为1;
是周期函数且其最小正周期为1;
② 函数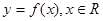 的图象关于点
的图象关于点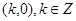 中心对称;
中心对称;
③ 函数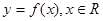 在
在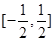 上单调递增;
上单调递增;
④ 方程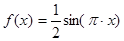 在
在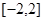 上共有7个不相等的实数根.
上共有7个不相等的实数根.
其中正确命题的序号是 .(写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com